実験データとは
次のように実験計画に基づき取得されたデータのことをいいます。[1]本例は、JMPのサンプルデータCustom RSM.jmpより。
| X1 | X2 | X3 | Y |
|---|---|---|---|
| -1 | -1 | -1 | 57.42 |
| 0 | 0 | 0 | 55.07 |
| 0 | -1 | 0 | 57.65 |
| -1 | 0 | 0 | 58.4 |
| 1 | 1 | -1 | 72.87 |
| 0 | 0 | 1 | 55.95 |
| 1 | -1 | 1 | 62.21 |
| -1 | 1 | -1 | 66.92 |
| 1 | 0 | 0 | 63.43 |
| 1 | -1 | -1 | 61.25 |
| -1 | 1 | 1 | 68.42 |
| 0 | 0 | -1 | 56.18 |
| 1 | 1 | 1 | 73.08 |
| -1 | -1 | 1 | 58.19 |
| 0 | 0 | 0 | 54.17 |
| 0 | 1 | 0 | 65.46 |
ここで、X1、X2、X3は因子、Yは特性です[2]モデリングを行うとき、因子は説明変数に、特性は目的変数に対応します。。実験計画に基づき、因子の値(水準)を変化させることによって、特性値に変化が生じています。
実験計画に基づき取得されたデータには、因子間の相関が小さいという特徴があります。本例でX1とX2の散布図を描くと、次のようになります。
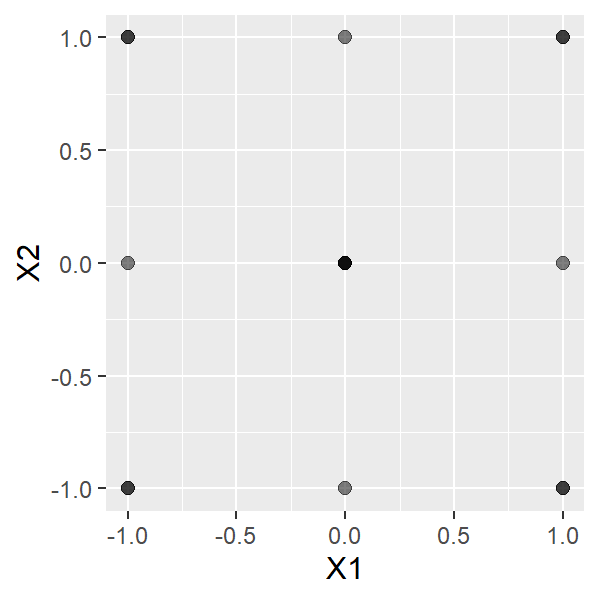
点がX1方向、X2方向ともに、等間隔に同じ数だけ配置されていることがわかります。このとき、X1とX2の相関係数はゼロです。X1とX3、X2とX3の相関係数も同様にゼロです。[3]因子間の相関係数がぴったりゼロになることが、実験計画の必要条件というわけではありません。
因子間の相関が小さいと、特性に対してどの因子の影響が大きいか、見極めが容易になるというメリットがあります。
また反復、無作為化、局所管理というフィッシャーの3原則に基づき実験を行うことで、系統誤差の影響を小さくすることができる、というメリットもあります。
観察データとは
観察データとは、実験データのように積極的に何かの因子を操作する(介入を行う)のではなく、自然の流れの中にあるものを観察したデータです。
観察データにおいては、因子間の相関が大きい状態がしばしば見られます。因子間の相関が大きいデータを用いてモデリングを行うと、多重共線性という問題が発生する場合があります。[4]多重共線性は、分散共分散行列の逆行列を求められない、あるいはその計算が不安定になるという問題です。詳しくは、別の記事でご説明します。
多重共線性はテクニカルな問題であるため、それを回避するために各種の手法が提案されてはいます。しかし相関の大きい因子間において、どちらがより特性に対して大きな影響を持つか、見極めが難しいということには変わりません。
極端な例ですが、上の実験計画において、X1とX2の値が完全に一致している場合を考えます。
| X1 | X2 | X3 | Y |
|---|---|---|---|
| -1 | -1 | -1 | 57.42 |
| 0 | 0 | 0 | 55.07 |
| 0 | 0 | 0 | 57.65 |
| -1 | -1 | 0 | 58.4 |
| 1 | 1 | -1 | 72.87 |
| 0 | 0 | 1 | 55.95 |
| 1 | 1 | 1 | 62.21 |
| -1 | -1 | -1 | 66.92 |
| 1 | 1 | 0 | 63.43 |
| 1 | 1 | -1 | 61.25 |
| -1 | -1 | 1 | 68.42 |
| 0 | 0 | -1 | 56.18 |
| 1 | 1 | 1 | 73.08 |
| -1 | -1 | 1 | 58.19 |
| 0 | 0 | 0 | 54.17 |
| 0 | 0 | 0 | 65.46 |
X1とX2の散布図を描くと、次のようになります。
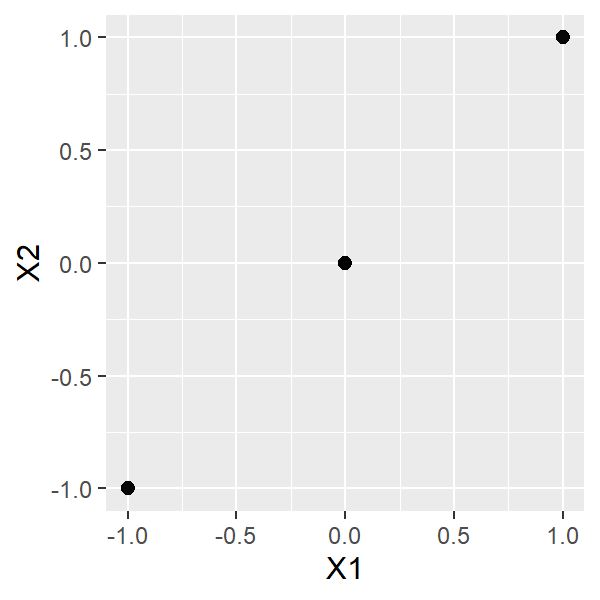
すべての点が、同一直線上に並んでいることがわかります。このとき、X1とX2の相関係数は1です。
X1とX2はまったく同じ情報を持っています。Yに対して、どちらがより大きな影響を持つか、データからは判断できないことが明らかです。
ここまで極端な例でなくても、因子間の相関が大きい場合には、それに似たことが起こるということです。
もし因果関係に興味があり、かつ実験の可能なテーマであれば、安易に観察データに頼るのではなく、積極的に実験データを取得することも検討すべきでしょう。



