ビッグデータとは
ビッグデータ(Big Data)とは何でしょうか?
この回答は、構造化データと非構造化データ、時系列データと非時系列データ、あるいは実験データと観察データについて語るより、ずっと困難です。
ビッグデータというのは、一種のバズワード[1]説得力を高めるためによく用いられているが、じつは無意味、または定義の曖昧な言葉。です。データ容量がいくら以上だとビッグデータだ、という決まりもありません。
ここではビッグデータについての直截的な回答を避け、スモールデータとの対比において、どのような傾向的特徴があるかについて見ていきたいと思います。
ビッグデータとスモールデータ
題材として、次のような構造化データを取り上げます。[2]本例は、Rにプリセットされているcarsデータセットより、ランダムで1/5行(10行)を抜き出したもの。
10行2列のデータです。speedは自動車の速度、distはブレーキを踏んでから止まるまでの距離(distance)を表しています。
| speed | dist |
|---|---|
| 4 | 2 |
| 7 | 22 |
| 12 | 24 |
| 13 | 34 |
| 14 | 80 |
| 18 | 76 |
| 18 | 56 |
| 20 | 32 |
| 20 | 64 |
| 25 | 85 |
散布図を描くと、次のようになります。
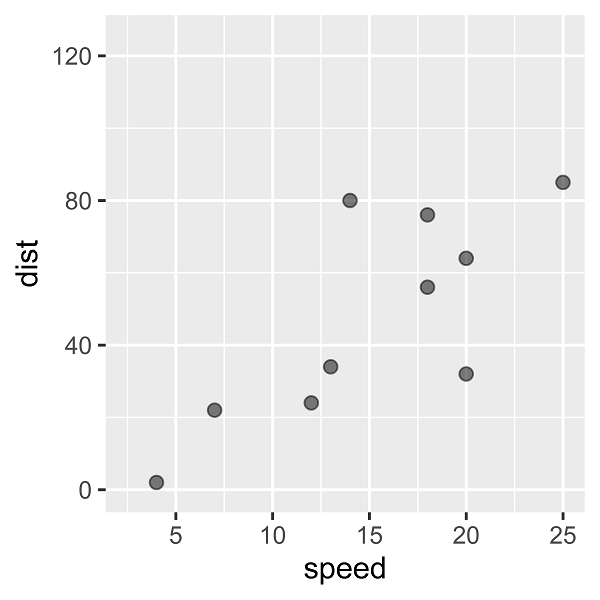
「speedからdistを予測する」というタスクを考えます。distを目的変数、speedを説明変数とした線形単回帰モデルをあてはめると、次のような回帰直線(予測式の直線)を描くことができます。
(既知のデータに対する)あてはまりの良さを表す指標として「決定係数」というものがありますが、このとき決定係数は0.592です。
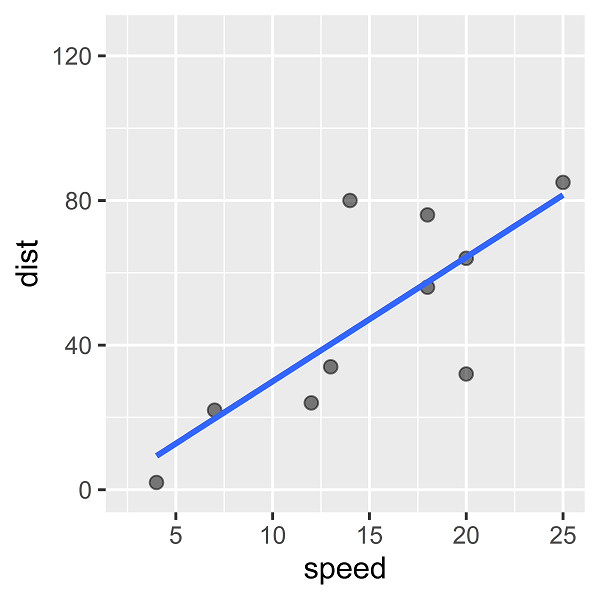
これを仮に「スモールデータ」だとして、データを大きくしていったときに、どのような特徴が現れるかを見ていきます。
ここで「データが大きい」といった場合、2つの方向性があります。
1つは「列数が大きい場合(列方向にデータが大きい場合)」、そしてもう1つは「行数が大きい場合(行方向にデータが大きい場合)」です。それぞれ、まったく異なった性質を持ちます。
列数が大きい場合
列数は、変数の数に対応しています。
目的変数は1つ(dist)として、説明変数の数が大きい場合を考えます。つまりspeedの他に、説明変数として使える変数があるような状況です。
ここでは便宜上、次のような多項式回帰モデルを想定し、多項式の次数を大きくしていくことを考えます。[3] … Continue reading
$$ y = \sum_{i=0}^k \beta_i x^i + \varepsilon $$
$ y $がdistに、$ x $がspeedに対応しています。$ i $は多項式の次数、$ \beta_i $は回帰係数($ i=0 $のとき定数項)、$ \varepsilon $は誤差です。
まず、speedの2次項「speed2」を追加した場合です。
| speed | speed2 | dist |
|---|---|---|
| 12 | 144 | 24 |
| 7 | 49 | 22 |
| 20 | 400 | 32 |
| 4 | 16 | 2 |
| 18 | 324 | 76 |
| 14 | 196 | 80 |
| 20 | 400 | 64 |
| 25 | 625 | 85 |
| 13 | 169 | 34 |
| 18 | 324 | 56 |
2次の多項式回帰モデルをあてはめると、次のような回帰曲線(予測式の曲線)を描くことができます。
このとき決定係数は0.6037と、線形単回帰モデルよりも(既知のデータに対する)あてはまりが良くなっています。
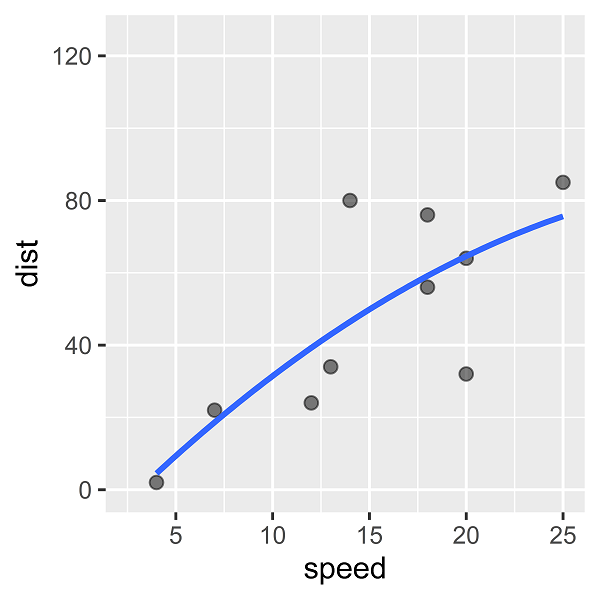
さらに、speedの3次項「speed3」を追加します。
| speed | speed2 | speed3 | dist |
|---|---|---|---|
| 12 | 144 | 1728 | 24 |
| 7 | 49 | 343 | 22 |
| 20 | 400 | 8000 | 32 |
| 4 | 16 | 64 | 2 |
| 18 | 324 | 5832 | 76 |
| 14 | 196 | 2744 | 80 |
| 20 | 400 | 8000 | 64 |
| 25 | 625 | 15625 | 85 |
| 13 | 169 | 2197 | 34 |
| 18 | 324 | 5832 | 56 |
3次の多項式回帰モデルをあてはめると、次のような回帰曲線を描くことができます。
このとき決定係数は0.6194と、2次の多項式モデルよりも(既知のデータに対する)あてはまりが良くなっています。
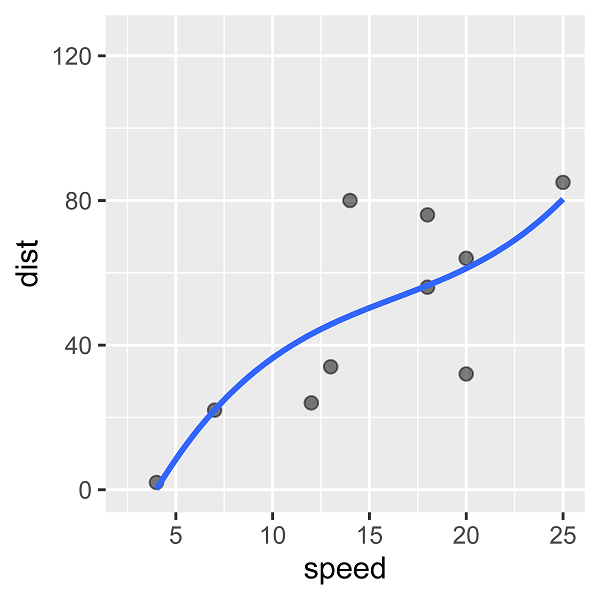
あとは同じことの繰り返しですので、speedの7次項(speed7)まで追加した状態を考えます。100,000を超える数字は省略して表示しています。
| speed | speed2 | speed3 | speed4 | speed5 | speed6 | speed7 | dist |
|---|---|---|---|---|---|---|---|
| 12 | 144 | 1728 | 20736 | 248832 | 3E+06 | 4E+07 | 24 |
| 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 22 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 32 |
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 2 |
| 18 | 324 | 5832 | 104976 | 2E+06 | 3E+07 | 6E+08 | 76 |
| 14 | 196 | 2744 | 38416 | 537824 | 8E+06 | 1E+08 | 80 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 64 |
| 25 | 625 | 15625 | 390625 | 1E+07 | 2E+08 | 6E+09 | 85 |
| 13 | 169 | 2197 | 28561 | 371293 | 5E+06 | 6E+07 | 34 |
| 18 | 324 | 5832 | 104976 | 2E+06 | 3E+07 | 6E+08 | 56 |
7次の多項式回帰モデルをあてはめると、次のような回帰曲線を描くことができます。
このとき決定係数は0.9027と、これまででもっとも高い値になっています。
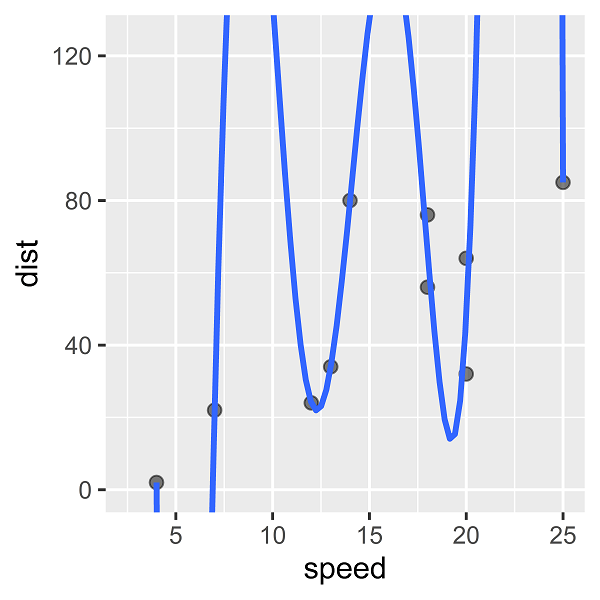
すべての点を縫うように、点の近傍を回帰曲線が通っていることがわかります。一方で、曲線は枠外にはみ出るくらい大きく波打っています。
確かに(既知のデータに対する)あてはまりはよいのですが、これを未知のデータ(speed)に対してdistを予測するモデルとして使って問題ないでしょうか?
例えば、speedが5のときdistがマイナスの値になる、あるいはspeedが10のときdistが120を超える値になるなどと、予測してよいでしょうか? ドメイン知識から判断して、そうならないことは明らかです。
これが過学習(overfitting)と呼ばれる問題です。列数が大きくなるほど、過学習が起こりやすくなります。[4]ドメイン知識だけでなく、過学習を抑制するための技術的な手法も存在します。
本例は比較的シンプルな例ですが、テーマによっては説明変数(特徴量)の数が数千、数万、あるいはそれ以上の場合も存在します。見えていないだけで、本例における「7次の多項式回帰モデル」のようなものを作っていた、ということが往々にしてあります。
行数が大きい場合
行数は、サンプルサイズ、観測値の数に対応しています。
これまで見てきたのは10行のデータでしたが、さらに観測を続け、全体で50行のデータを得られたとします。
| speed | dist |
|---|---|
| 4 | 2 |
| 4 | 10 |
| 7 | 4 |
| 7 | 22 |
| 8 | 16 |
| 9 | 10 |
| 10 | 18 |
| 10 | 26 |
| 10 | 34 |
| 11 | 17 |
| 11 | 28 |
| 12 | 14 |
| 12 | 20 |
| 12 | 24 |
| 12 | 28 |
| 13 | 26 |
| 13 | 34 |
| 13 | 34 |
| 13 | 46 |
| 14 | 26 |
| 14 | 36 |
| 14 | 60 |
| 14 | 80 |
| 15 | 20 |
| 15 | 26 |
| 15 | 54 |
| 16 | 32 |
| 16 | 40 |
| 17 | 32 |
| 17 | 40 |
| 17 | 50 |
| 18 | 42 |
| 18 | 56 |
| 18 | 76 |
| 18 | 84 |
| 19 | 36 |
| 19 | 46 |
| 19 | 68 |
| 20 | 32 |
| 20 | 48 |
| 20 | 52 |
| 20 | 56 |
| 20 | 64 |
| 22 | 66 |
| 23 | 54 |
| 24 | 70 |
| 24 | 92 |
| 24 | 93 |
| 24 | 120 |
| 25 | 85 |
散布図を描くと、次のようになります。
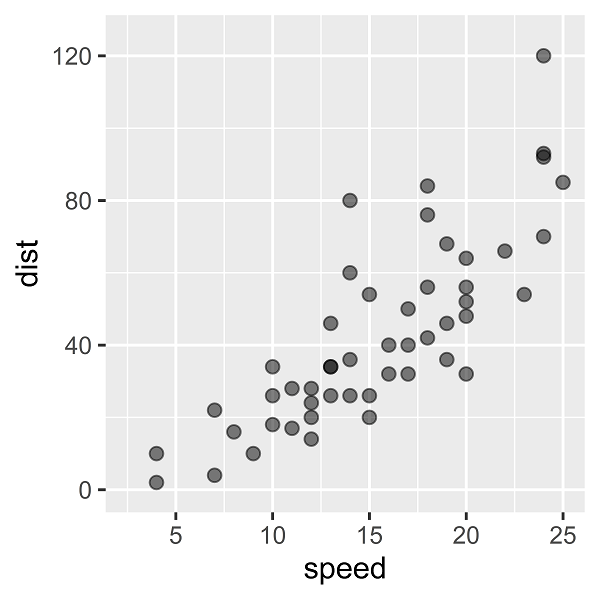
線形単回帰モデルをあてはめると、次のような回帰直線を描くことができます。
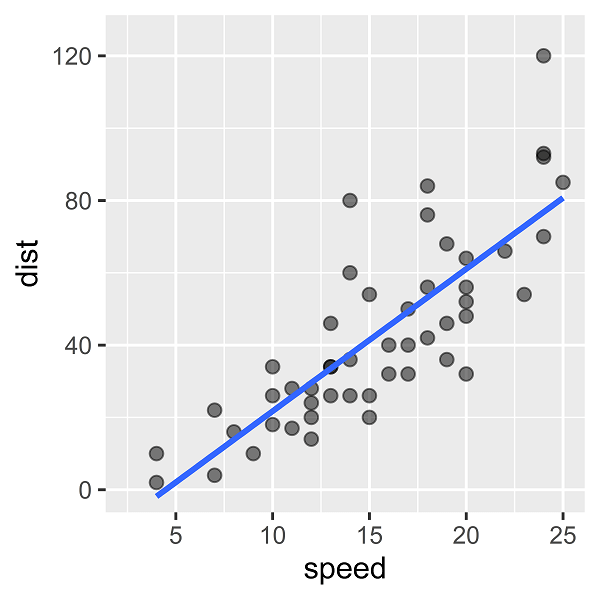
さらに、2次の多項式回帰モデルをあてはめると、次のような回帰曲線を描くことができます。表は省略します。
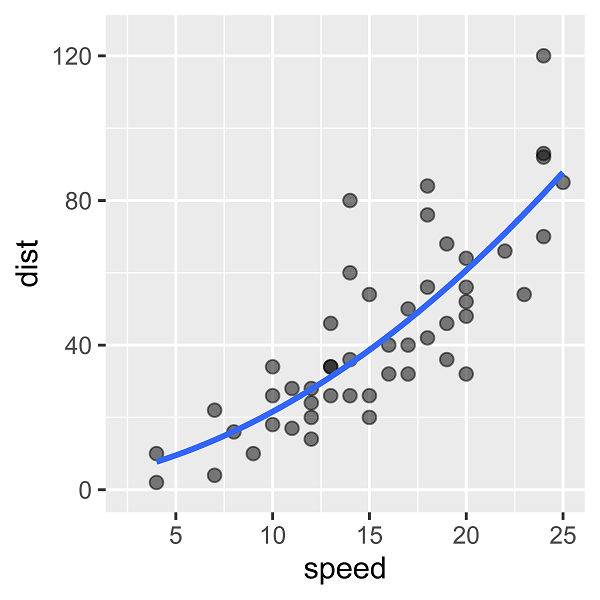
下に膨らんだような曲線になっています。10行のデータを使った場合は、上に膨らんだような曲線になっていました。どちらが正しいのでしょうか?
(正しくサンプリングが行われていることを前提として)行数が大きくなるほど、当然ですが標本(観測値の集合)の特性は、母集団の特性に近づく傾向にあります。
本例ではドメイン知識からも、下に膨らんだような曲線になるはずだ、ということがいえます。
また統計解析では仮説検定というフレームワークを利用しますが、行数が大きくなるほど統計的有意性の判断が難しくなる、という点には注意が必要です。
列数も行数も大きい場合
最後に考えるのは、列数と行数、どちらも大きい場合です。
50行のデータを得られ、かつspeedの7次項(speed7)まで追加した状態を考えます。100,000を超える数字は省略して表示しています。
| speed | speed2 | speed3 | speed4 | speed5 | speed6 | speed7 | dist |
|---|---|---|---|---|---|---|---|
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 2 |
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 10 |
| 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 4 |
| 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 22 |
| 8 | 64 | 512 | 4096 | 32768 | 262144 | 2E+06 | 16 |
| 9 | 81 | 729 | 6561 | 59049 | 531441 | 5E+06 | 10 |
| 10 | 100 | 1000 | 10000 | 100000 | 1E+06 | 1E+07 | 18 |
| 10 | 100 | 1000 | 10000 | 100000 | 1E+06 | 1E+07 | 26 |
| 10 | 100 | 1000 | 10000 | 100000 | 1E+06 | 1E+07 | 34 |
| 11 | 121 | 1331 | 14641 | 161051 | 2E+06 | 2E+07 | 17 |
| 11 | 121 | 1331 | 14641 | 161051 | 2E+06 | 2E+07 | 28 |
| 12 | 144 | 1728 | 20736 | 248832 | 3E+06 | 4E+07 | 14 |
| 12 | 144 | 1728 | 20736 | 248832 | 3E+06 | 4E+07 | 20 |
| 12 | 144 | 1728 | 20736 | 248832 | 3E+06 | 4E+07 | 24 |
| 12 | 144 | 1728 | 20736 | 248832 | 3E+06 | 4E+07 | 28 |
| 13 | 169 | 2197 | 28561 | 371293 | 5E+06 | 6E+07 | 26 |
| 13 | 169 | 2197 | 28561 | 371293 | 5E+06 | 6E+07 | 34 |
| 13 | 169 | 2197 | 28561 | 371293 | 5E+06 | 6E+07 | 34 |
| 13 | 169 | 2197 | 28561 | 371293 | 5E+06 | 6E+07 | 46 |
| 14 | 196 | 2744 | 38416 | 537824 | 8E+06 | 1E+08 | 26 |
| 14 | 196 | 2744 | 38416 | 537824 | 8E+06 | 1E+08 | 36 |
| 14 | 196 | 2744 | 38416 | 537824 | 8E+06 | 1E+08 | 60 |
| 14 | 196 | 2744 | 38416 | 537824 | 8E+06 | 1E+08 | 80 |
| 15 | 225 | 3375 | 50625 | 759375 | 1E+07 | 2E+08 | 20 |
| 15 | 225 | 3375 | 50625 | 759375 | 1E+07 | 2E+08 | 26 |
| 15 | 225 | 3375 | 50625 | 759375 | 1E+07 | 2E+08 | 54 |
| 16 | 256 | 4096 | 65536 | 1E+06 | 2E+07 | 3E+08 | 32 |
| 16 | 256 | 4096 | 65536 | 1E+06 | 2E+07 | 3E+08 | 40 |
| 17 | 289 | 4913 | 83521 | 1E+06 | 2E+07 | 4E+08 | 32 |
| 17 | 289 | 4913 | 83521 | 1E+06 | 2E+07 | 4E+08 | 40 |
| 17 | 289 | 4913 | 83521 | 1E+06 | 2E+07 | 4E+08 | 50 |
| 18 | 324 | 5832 | 104976 | 2E+06 | 3E+07 | 6E+08 | 42 |
| 18 | 324 | 5832 | 104976 | 2E+06 | 3E+07 | 6E+08 | 56 |
| 18 | 324 | 5832 | 104976 | 2E+06 | 3E+07 | 6E+08 | 76 |
| 18 | 324 | 5832 | 104976 | 2E+06 | 3E+07 | 6E+08 | 84 |
| 19 | 361 | 6859 | 130321 | 2E+06 | 5E+07 | 9E+08 | 36 |
| 19 | 361 | 6859 | 130321 | 2E+06 | 5E+07 | 9E+08 | 46 |
| 19 | 361 | 6859 | 130321 | 2E+06 | 5E+07 | 9E+08 | 68 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 32 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 48 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 52 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 56 |
| 20 | 400 | 8000 | 160000 | 3E+06 | 6E+07 | 1E+09 | 64 |
| 22 | 484 | 10648 | 234256 | 5E+06 | 1E+08 | 2E+09 | 66 |
| 23 | 529 | 12167 | 279841 | 6E+06 | 1E+08 | 3E+09 | 54 |
| 24 | 576 | 13824 | 331776 | 8E+06 | 2E+08 | 5E+09 | 70 |
| 24 | 576 | 13824 | 331776 | 8E+06 | 2E+08 | 5E+09 | 92 |
| 24 | 576 | 13824 | 331776 | 8E+06 | 2E+08 | 5E+09 | 93 |
| 24 | 576 | 13824 | 331776 | 8E+06 | 2E+08 | 5E+09 | 120 |
| 25 | 625 | 15625 | 390625 | 1E+07 | 2E+08 | 6E+09 | 85 |
7次の多項式回帰モデルをあてはめると、次のような回帰曲線を描くことができます。
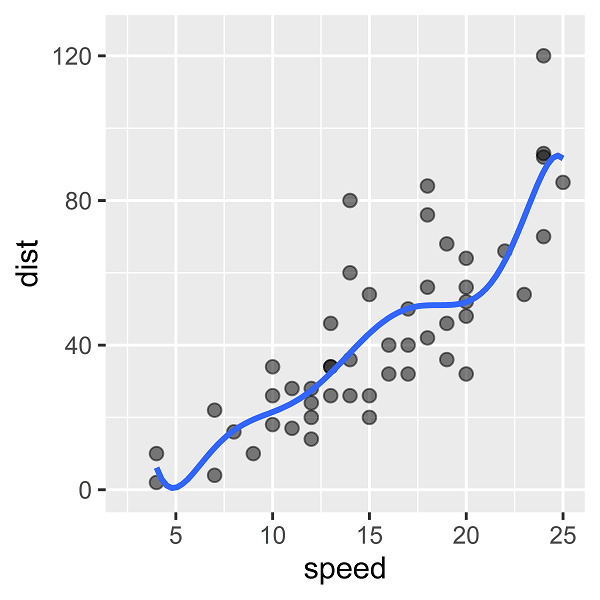
10行のデータでは枠外にはみ出るほど大きく波打っていたのが、50行のデータだと波の高さがかなり抑えれてされていることがわかります。
列数が大きくなるほど、過学習しやすくなることは上でお伝えした通りですが、一方で行数が大きくなるほど、過学習を抑制する効果が働きます。気にするべきは、列数と行数のバランスです。
ここで、50行のデータがあれば7次の多項式回帰モデルをあてはめるべきだ、といっているわけではありません[5]本例では、distを平方根変換した上で線形単回帰モデルをあてはめるのが、ベストな解法ではないでしょうか。。7次の多項式回帰モデルのように(無駄に)モデルを複雑にしたとしても、行数が大きければすくなくとも、極端な過学習を回避することができるということです。

脚注


