ベクトルとは
ベクトル(vector)とは、大きさと向きを持つ量を表す数学的な概念です。対して、大きさのみを持つ量をスカラー(scalar)と呼びます。
2次元ベクトルは、次のように数式で表されます[1]ベクトルには本例のように太字で表す記法と、\(\vec{a}\) のように文字の上に矢印をつけて表す記法が存在します。。ここで、\(a_1\)、\(a_2\) はスカラーです。
\[
\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}
\]
例えば \(\mathbf{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\) は、次のように図示することができます[2]3次元以上のベクトルも、2次元ベクトルと同じように大きさと向きを持ちますが、2次元平面上には表現することができません。。
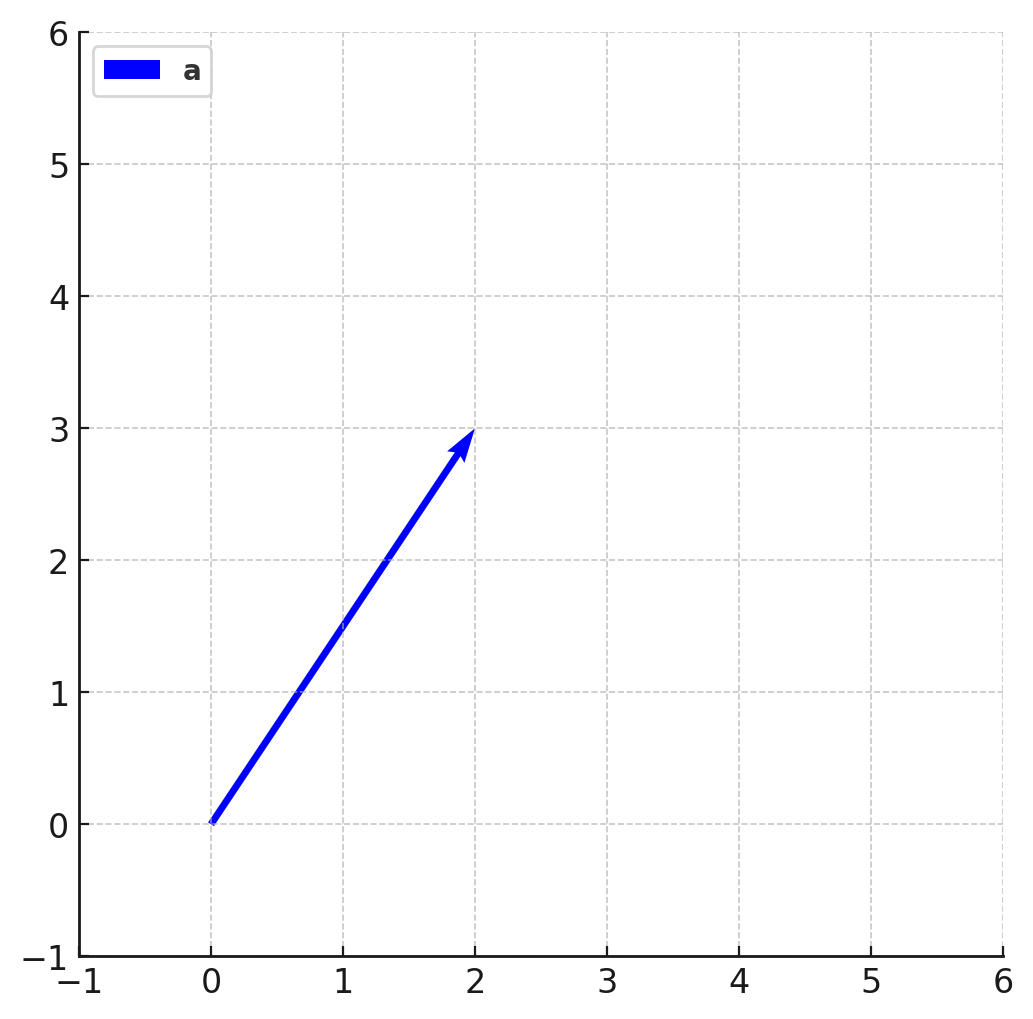
ニューラルネットワークモデルにおける入力ベクトル、出力ベクトル、バイアスベクトル、また大規模言語モデル(LLM)における埋め込みベクトル、キー・クエリ・バリューベクトルなど、ベクトルはデータサイエンスにおける基盤的な概念のひとつです。
行ベクトルと列ベクトル
ベクトルは通常、列ベクトルとして表現されますが、行ベクトルとして表現することも可能です。
列ベクトルは、次のように表されます。
\[
\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}
\]
行ベクトルは、次のように表されます。
\[
\mathbf{a}^T = \begin{pmatrix} a_1 & a_2 & \cdots & a_n \end{pmatrix}
\]
ここで上付きの \(T\) は、列と行を変換する転置(transpose)の記号です[3] … Continue reading。
ベクトルの和と差
2次元ベクトル \(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\)、\(\mathbf{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}\) の和と差は、次のように計算できます。
\[
\begin{aligned}
\mathbf{a} + \mathbf{b} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \end{pmatrix} \\
\mathbf{a} \mathbin{-} \mathbf{b} = \begin{pmatrix} a_1 \mathbin{-} b_1 \\ a_2 \mathbin{-} b_2 \end{pmatrix}
\end{aligned}
\]
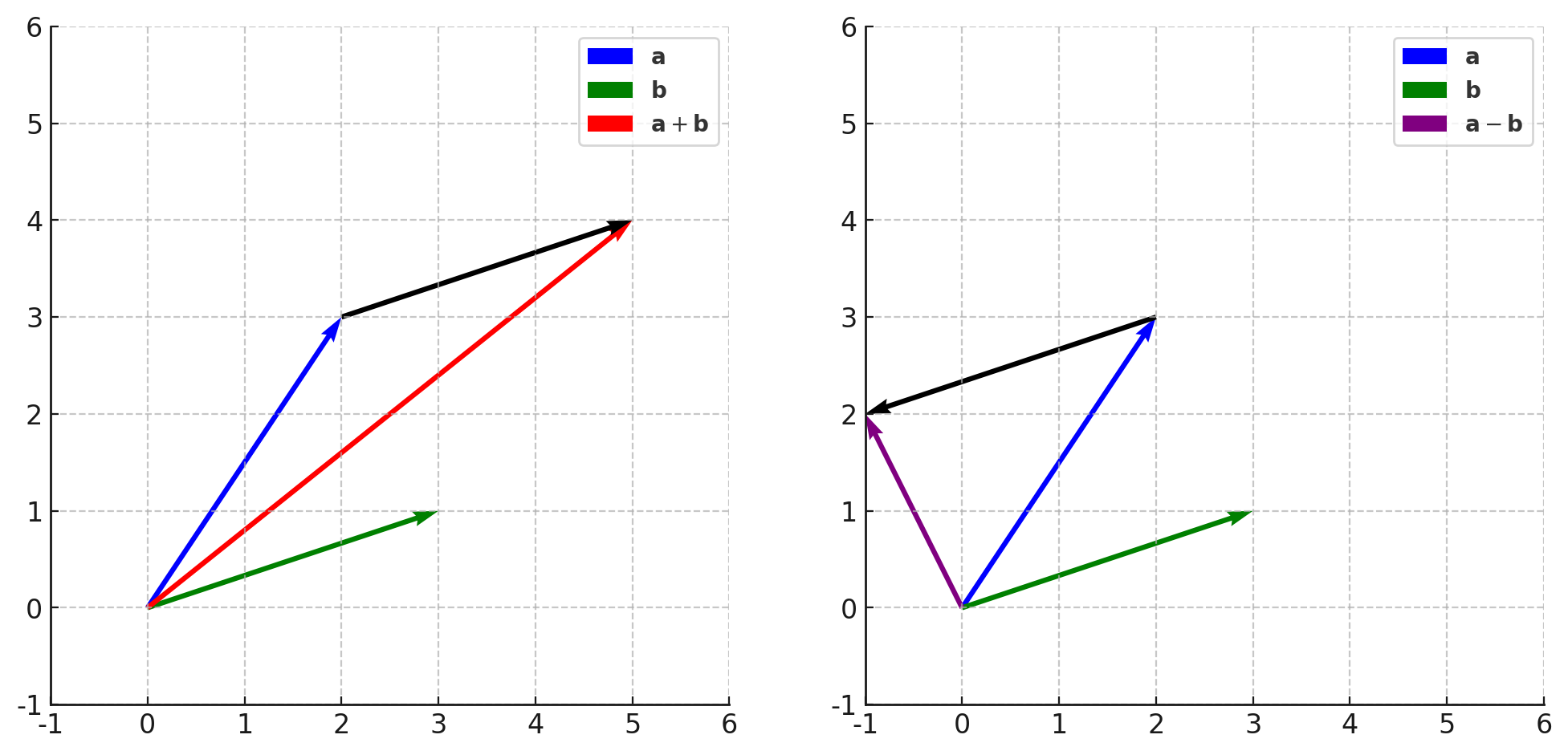
例えば \(\mathbf{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\)、\(\mathbf{b} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}\) の和と差は、次のように計算できます。
\[
\begin{aligned}
\mathbf{a} + \mathbf{b} = \begin{pmatrix} 2 + 3 \\ 3 + 1 \end{pmatrix} = \begin{pmatrix} 5 \\ 4 \end{pmatrix} \\
\mathbf{a} \mathbin{-} \mathbf{b} = \begin{pmatrix} 2 \mathbin{-} 3 \\ 3 \mathbin{-} 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 2 \end{pmatrix}
\end{aligned}
\]
\(\mathbf{a} + \mathbf{b}\) は、\(\mathbf{a}\) の終点から \(\mathbf{b}\) をつなげたベクトルとして視覚的に表現できます。\(\mathbf{a} \mathbin{-} \mathbf{b}\) は、\(\mathbf{b}\) を逆向きにして \(\mathbf{a}\) の終点につなげたベクトルです。
ノルム
ノルム(norm)は、ベクトルの大きさ(長さ)を意味します。
ノルムの定義(2次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\) のノルムは、次のように定義されます[4]ここでノルムは、ユークリッドノルム(L2ノルム)を意味します。。
\[
\|\mathbf{a}\| = \sqrt{a_1^2 + a_2^2}
\]
例えば \(\mathbf{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\) のノルムは、次のように計算されます。
\[
\|\mathbf{a}\| = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.605
\]
ノルムの定義(n次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}\) のノルムは、次のように定義されます。
\[
\|\mathbf{a}\| = \sqrt{a_1^2 + a_2^2 + \cdots + a_n^2} = \sqrt{ \sum_{i=1}^{n} a_i^2 }
\]
ノルムについて詳しくは、下の記事をご参照ください。

ベクトルの正規化
正規化(normalization)とは、ベクトルのノルム(大きさ)を 1 にする操作を指します。正規化されたベクトルを、単位ベクトル(unit vector)と呼びます。
ベクトルをノルムで割ることで、単位ベクトル \(\hat{\mathbf{a}}\) を求めることができます。
\[
\hat{\mathbf{a}} = \frac{\mathbf{a}}{\|\mathbf{a}\|}
\]
例えば \(\mathbf{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\) の単位ベクトルは、次のように計算されます。
\[
\hat{\mathbf{a}} = \frac{\mathbf{a}}{\|\mathbf{a}\|} = \frac{1}{\sqrt{13}} \begin{pmatrix} 2 \\ 3 \end{pmatrix} \approx \begin{pmatrix} 0.5547 \\ 0.8321 \end{pmatrix}
\]
コサイン類似度を求める場合など、ベクトルの方向のみを重視する場合に、ベクトルの正規化が用いられます。
内積
内積(dot product)とは、2つのベクトルの掛け算に相当する演算です。内積はスカラーを返します。
内積の定義(2次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\)、\(\mathbf{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}\) の内積は、次のように定義されます。
\[
\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2
\]
例えば \(\mathbf{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\)、\(\mathbf{b} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}\) の内積は、次のように計算されます。
\[
\mathbf{a} \cdot \mathbf{b} = 2 \times 3 + 3 \times 1 = 6 + 3 = 9
\]
内積の定義(n次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}\)、\(\mathbf{b} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}\) の内積は、次のように定義されます。
\[
\mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + \cdots + a_nb_n = \sum_{i=1}^{n} a_i b_i
\]
内積について詳しくは、下の記事をご参照ください。

ベクトルの公式(2次元)
- ベクトルのスカラー倍 $$ k\mathbf{a} = \begin{pmatrix} ka_1 \\ ka_2 \end{pmatrix} $$
- ベクトルの和 $$ \mathbf{a} + \mathbf{b} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \end{pmatrix} $$
- ベクトルの差 $$ \mathbf{a} \mathbin{-} \mathbf{b} = \begin{pmatrix} a_1 \mathbin{-} b_1 \\ a_2 \mathbin{-} b_2 \end{pmatrix} $$
ベクトルの公式(n次元)
- ベクトルのスカラー倍 $$ k\mathbf{a} = \begin{pmatrix} ka_1 \\ ka_2 \\ \vdots \\ ka_n \end{pmatrix} $$
- ベクトルの和 $$ \mathbf{a} + \mathbf{b} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \\ \vdots \\ a_n + b_n \end{pmatrix} $$
- ベクトルの差 $$ \mathbf{a} \mathbin{-} \mathbf{b} = \begin{pmatrix} a_1 \mathbin{-} b_1 \\ a_2 \mathbin{-} b_2 \\ \vdots \\ a_n \mathbin{-} b_n \end{pmatrix} $$
