ノルムとは
ノルム(norm)とは、ベクトルの大きさ(長さ)を表す数学的な概念です。ノルムには様々な種類がありますが、特に重要なものとして、マンハッタンノルム(L1ノルム)とユークリッドノルム(L2ノルム)があります[1]単に「ノルム」といった場合、ユークリッドノルムを意味する場合が多いです。。
例えば下図のように、原点と座標 \((4, 3)\) との距離を考えるとき、水平移動・垂直移動の距離がマンハッタンノルム(マンハッタン距離)[2] … Continue reading、斜め移動の距離がユークリッドノルム(ユークリッド距離)です。
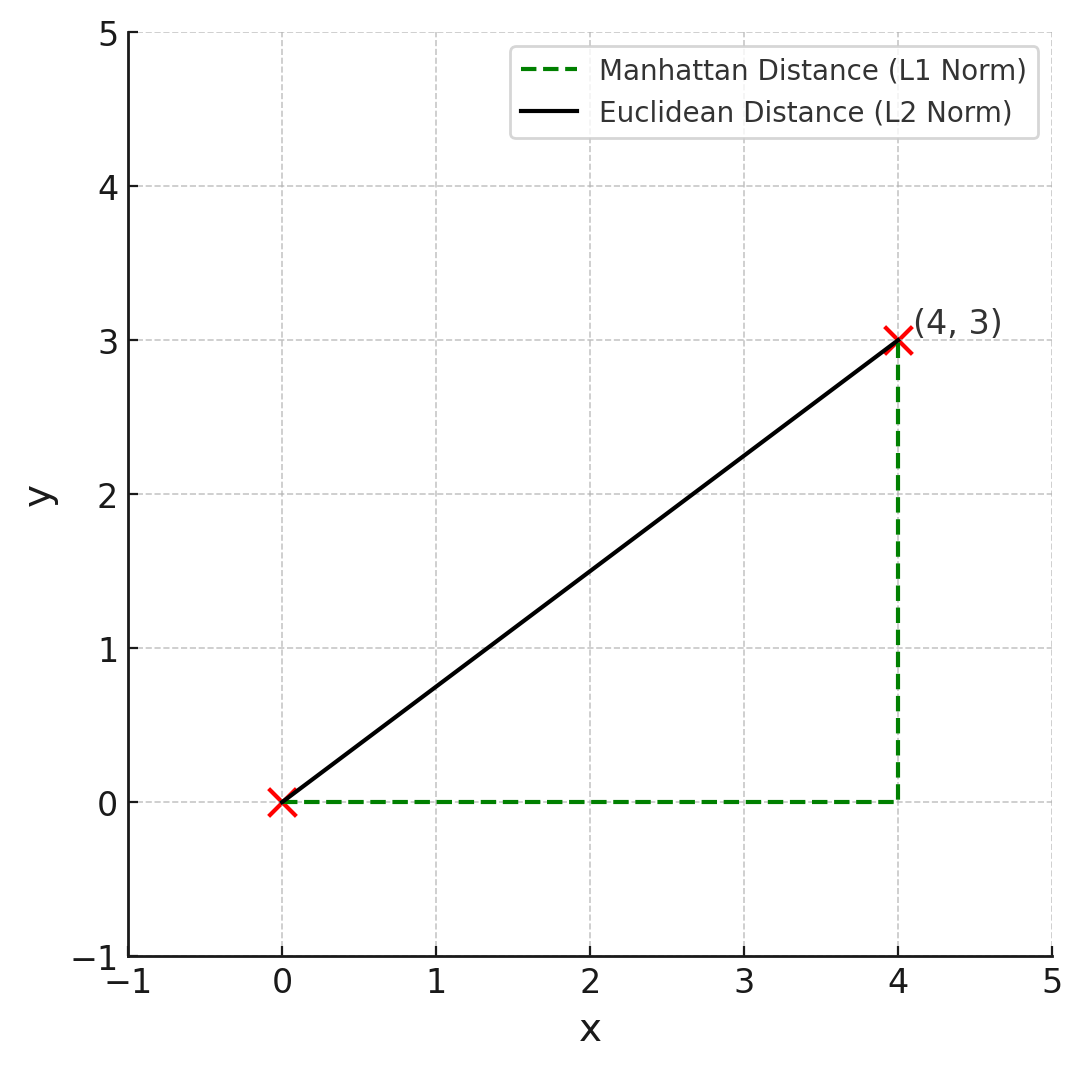
ノルムは、機械学習モデルの正則化(L1正則化、L2正則化)、階層型クラスター分析、k-平均法(k-means)、k-近傍法(k-NN)など、データサイエンスの様々な場面で用いられます。
マンハッタンノルム(L1ノルム)
マンハッタンノルム(Manhattan norm)は、ベクトルの各成分の絶対値の総和として定義されます。L1ノルムとも呼ばれます。
マンハッタンノルムの定義(2次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\) のマンハッタンノルムは、次のように定義されます。
\[
\|\mathbf{a}\|_1 = |a_1| + |a_2|
\]
例えば \(\mathbf{a} = \begin{pmatrix} 4 \\ 3 \end{pmatrix}\) のマンハッタンノルムは、次のように計算されます。
\[
\|\mathbf{a}\|_1 = |4| + |3| = 4 + 3 = 7
\]
マンハッタンノルムの定義(n次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}\) のマンハッタンノルムは、次のように定義されます。
\[
\|\mathbf{a}\|_1 = \sum_{i=1}^{n} |a_i|
\]
ユークリッドノルム(L2ノルム)
ユークリッドノルム(Euclidean norm)は、ベクトルの各成分の二乗和の平方根として定義されます。L2ノルムとも呼ばれます。
ユークリッドノルムの定義(2次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\) のユークリッドノルムは、次のように定義されます。
\[
\|\mathbf{a}\|_2 = \sqrt{a_1^2 + a_2^2}
\]
例えば \(\mathbf{a} = \begin{pmatrix} 4 \\ 3 \end{pmatrix}\) のユークリッドノルムは、次のように計算されます。
\[
\|\mathbf{a}\|_2 = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5
\]
ユークリッドノルムの定義(n次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}\) のユークリッドノルムは、次のように定義されます。
\[
\|\mathbf{a}\|_2 = \sqrt{\sum_{i=1}^{n} a_i^2}
\]
p-ノルム
p-ノルムは、マンハッタンノルム(L1ノルム)やユークリッドノルム(L2ノルム)を含む概念として、一般化して定義されたノルムです。
- p = 1 のとき、マンハッタンノルム(L1ノルム)
- p = 2 のとき、ユークリッドノルム(L2ノルム)
- p → ∞ のとき、チェビシェフノルム(最大値ノルム)
p-ノルムの定義(2次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\) の p-ノルムは次のように定義されます。
\[
\|\mathbf{a}\|_p = \left( |a_1|^p + |a_2|^p \right)^{\frac{1}{p}}
\]
p-ノルムの定義(n次元)
\(\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}\) の p-ノルムは次のように定義されます。
\[
\|\mathbf{a}\|_p = \left(\sum_{i=1}^{n} |a_i|^p \right)^{\frac{1}{p}}
\]

