対数とは
対数とは、ある数(底)を何回かければ(何乗すれば)目的の数(真数)になるかを表す数学的な概念です。式で表すと、次のようになります。\( b \) を底、\( x \) を真数と呼び、その対数の値が \( y \) です[1]対数の真数を \( x \) を変数とした関数 \( f(x) = \log_b x \) が 対数関数です。。
$$ \log_b x = \log_b b^y = y $$
例えば、\( 10 \) を底、\( 1000 \) を真数とする対数の値は \( 3 \) です。
$$ \log_{10} 1000 = \log_{10} 10^3 = 3 $$
対数は底の違いにより、次のように呼び分けられています。
| 記法 | 名称 | 主な用途 |
|---|---|---|
| \( \log_e x = \ln x \) | 自然対数 | 対数正規分布、対数尤度など |
| \( \log_{10} x \) | 常用対数 | 片対数グラフ、両対数グラフなど |
| \( \log_{2} x \) | 二進対数 | 情報理論(ビット)など |
自然対数(Natural logarithm)は底をネイピア数 \( e \) とした場合で、数学上の取り扱いがしやすく、データサイエンスではもっともよく用いられています。\( \ln \) という記号を用いて表すのが一般的です。
常用対数(Common logarithm)はデシベル(dB)という単位に代表されるような、10の累乗で大きくなるようなデータから桁を取り出す場合などに用いられます[2]歴史的経緯から常用対数と呼ばれているものの、データサイエンスにおいては自然対数のほうが「常用」されています。。
二進対数(Binary logarithm)は情報理論において、情報量、エントロピー、ダイバジェーンスをビット(bit)の単位で計算する場合などに用いられます。
対数のグラフ
自然対数、常用対数、二進対数をグラフで表すと、次のようになります。
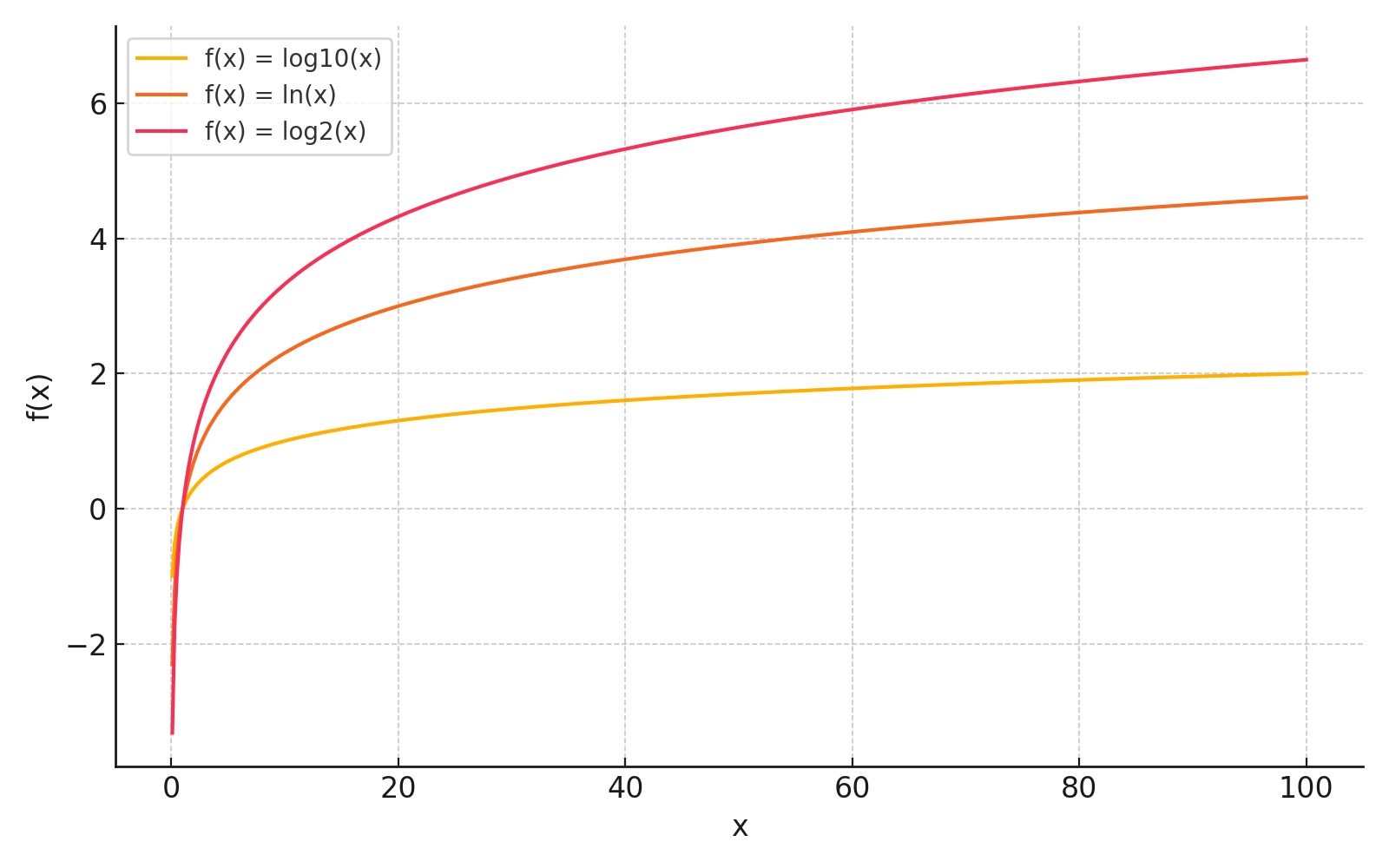
対数の性質
\( b^0 = 1 \) より、真数が \( 1 \) のとき対数の値は \( 0 \) になります。
$$ \log_b 1 = 0 \quad (b > 0, b \neq 1) $$
また下記式は一見複雑ですが、「\( e \) を何乗すれば \( a \) になるか」を対数記号で表したのが \( \ln a \) のため、公式というよりは対数の定義そのものです。
$$ a = e^{\ln a} \quad (a > 0) $$
さらに両辺を \( x \) 乗すれば、下記式になります[3]一般指数関数の微分の公式を導出する場合などに、本式変形が用いられます。。
$$ a^x = e^{x \ln a} \quad (a > 0) $$
対数の公式
- 積の対数 $$ \log_b(xy) = \log_b x + \log_b y \quad (x > 0, y > 0, b > 0, b \neq 1) $$
- 商の対数 $$ \log_b\left(\frac{x}{y}\right) = \log_b x \mathbin{-} \log_b y \quad (x > 0, y > 0, b > 0, b \neq 1) $$
- 累乗の対数 $$ \log_b(x^r) = r \log_b x \quad (x > 0, b > 0, b \neq 1) $$
- 底の変換 $$ \log_b x = \frac{\log_k x}{\log_k b} \quad (x > 0, b > 0, b \neq 1, k > 0, k \neq 1) $$

