積分とは
積分とは、関数の変化を積み重ねてその全体量を求める数学的な概念です。データサイエンスにおいては、確率を確率密度関数の積分として求めます（連続確率分布の場合）。ベイズ推定における周辺尤度（エビデンス）の計算にも積分が用いられます[1] … Continue reading。
不定積分
不定積分とは、微分（導関数を求める操作）の逆を考えるもので、以下のように表されます。
\[
\int f(x) \,dx = F(x) + C
\]
ここで、\( F(x) \) または \( F(x) + C \) は \( f(x) \) の原始関数であり、\( C \) は任意の積分定数です。定数を微分すると \( 0 \) となるため、積分定数の違いにより原始関数は無数に存在します[2]不定積分は（無数に存在する）原始関数の総称である、といった説明がされる場合もあります。。
定積分
定積分とは、ある区間 \( [a, b] \) における関数 \( f(x) \) と \( x \) 軸との間の面積を求めるものです。数式で表すと、次のようになります。
\[
\int_{a}^{b} f(x) \,dx = \left[ F(x) \right]_{a}^{b} = F(b) – F(a)
\]
以下のグラフは、関数 \( f(x) = x^2 \) の区間 \( [0.5, 1.5] \) における定積分を可視化したものです。
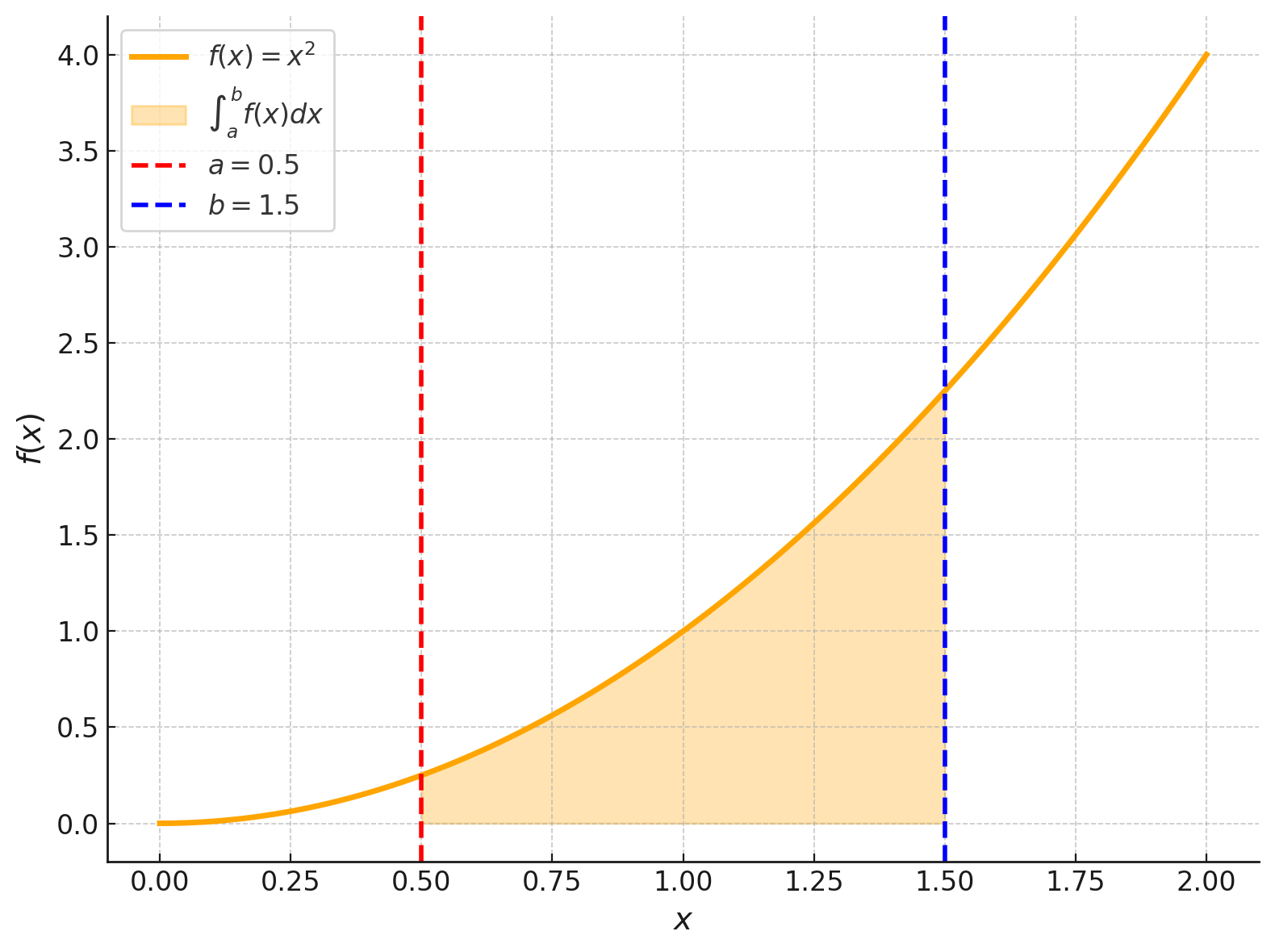
関数 $ f(x) = x^2 $ の区間 $ [0.5, 1.5] $ における定積分は、次のように計算できます。
まず、$ x^2 $ の不定積分を求めます。
\begin{align*}
\int x^2 \,dx &= \frac{x^3}{3} + C
\end{align*}
ここで、$ F(x) = \frac{x^3}{3} $ とすると、定積分の公式を適用して次のように計算できます。
\begin{align*}
\int_{0.5}^{1.5} x^2 \,dx = \left[ F(x) \right]_{0.5}^{1.5} &= F(1.5) – F(0.5) \\
&= \left( \frac{(1.5)^3}{3} \right) – \left( \frac{(0.5)^3}{3} \right) \\
&= 1.0833 \quad \text{(小数第4位まで)}
\end{align*}
積分の公式
- 定数の積分 $$ \int c \mathrm{d}x = cx + C $$
- べき乗の積分 $$ \int x^n \mathrm{d}x = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1) $$
- 自然指数関数の積分 $$ \int e^x \mathrm{d}x = e^x + C $$
- 一般指数関数の積分 $$ \int a^x \mathrm{d}x = \frac{a^x}{\ln a} + C \quad (a > 0, a \neq 1) $$
- 自然対数関数の積分 $$ \int \frac{1}{x} \mathrm{d}x = \ln |x| + C $$
- 一般対数関数の積分: $$ \int \frac{1}{x \ln a} \, \mathrm{d}x = \log_a |x| + C \quad (a > 0, a \neq 1) $$
