指数とは
指数とは、ある数（底）を何回かけるか（何乗するか）を表す数学的な概念です。式で表すと、次のようになります。\( a \) を底、\( x \) を指数と呼びます[1]指数 \( x \) を変数とした関数 \( f(x) = a^x \) が指数関数です。。
$$ a^x = \underbrace{a \times a \times \cdots \times a}_{x\ \text{回}} $$
例えば、\( 10^3 \) は \( 10 \) を \( 3 \) 回かける（ \( 3 \) 乗する）ことを意味します。
$$ 10^3 = \underbrace{10 \times 10 \times 10}_{3\ \text{回}} $$
データサイエンスにおいて、指数分布や正規分布などの確率密度関数、分類問題における出力層としてのシグモイド関数やソフトマックス関数など、様々な場面で指数が用いられます。
指数のグラフ
\( 2^x \)、\( e^x \)、\( 10^x \) をグラフで表すと、次のようになります。
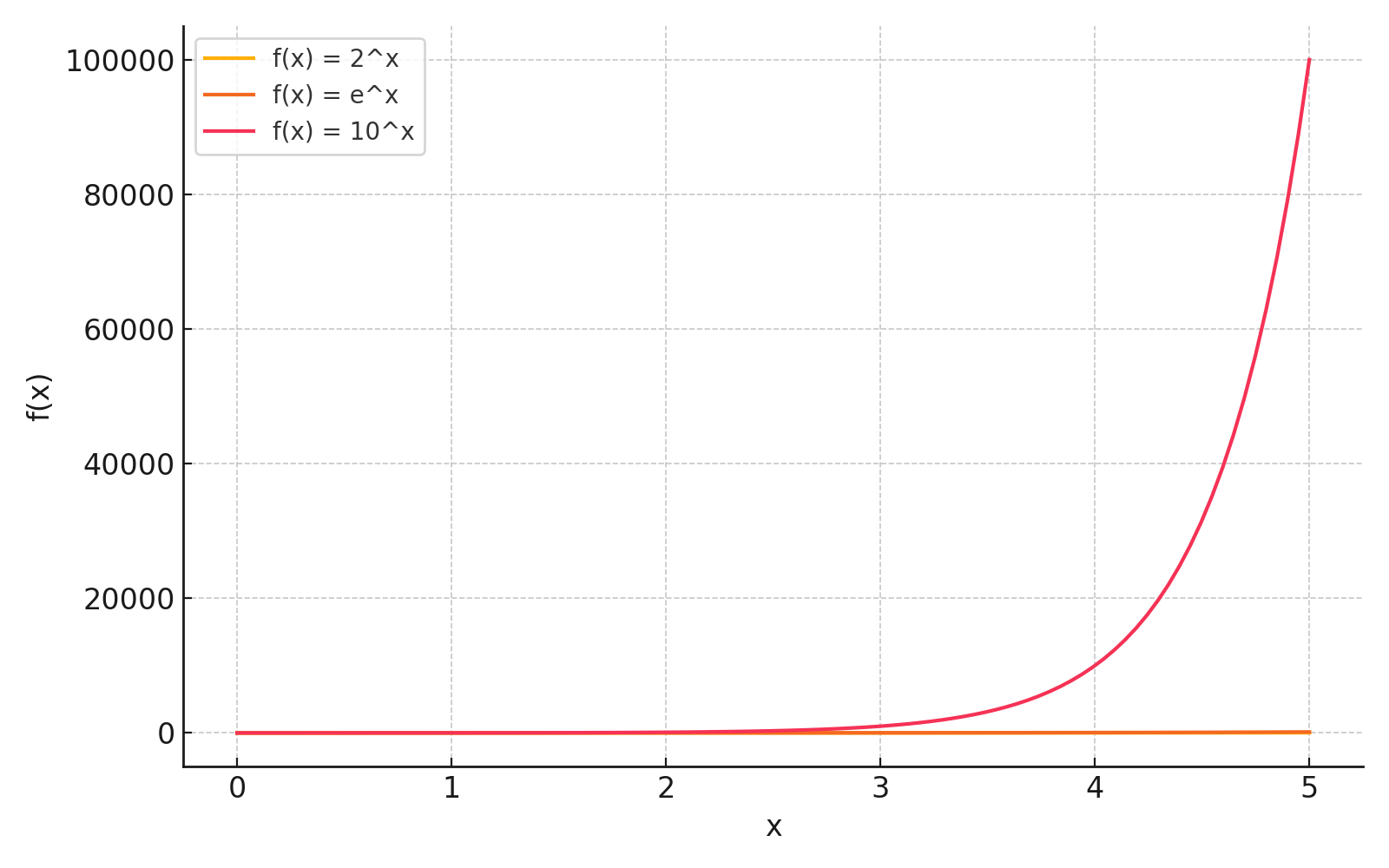
\( 2^x \)、\( e^x \) の変化が見えないため、縦軸を \( \log_{10} \) の対数スケールにした片対数グラフを下に示します。
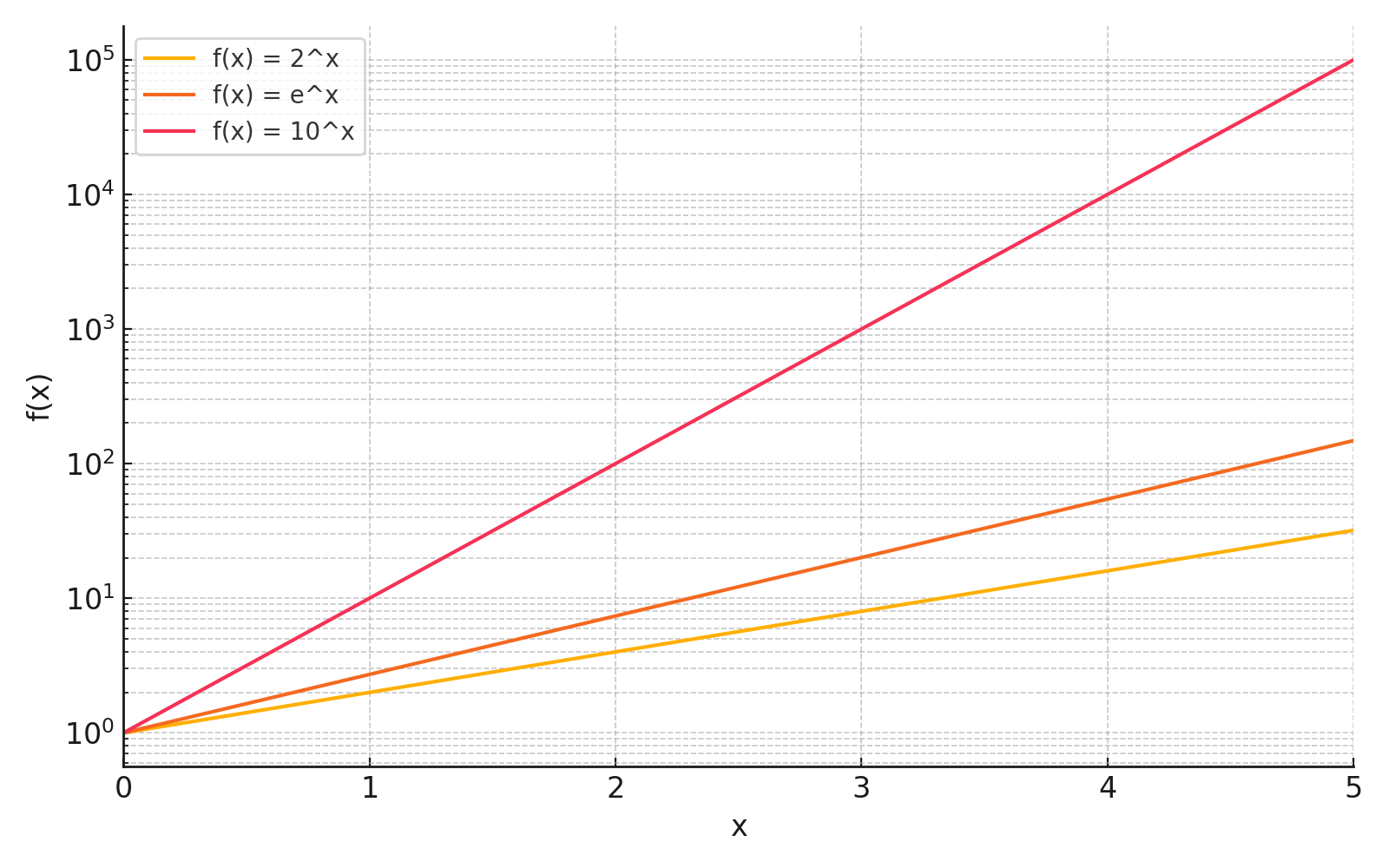
指数の性質
指数を \( 0 \) とした \( a^0 \) の値は \( 1 \) になります。
$$ a^0 = 1 \quad (a \neq 0) $$
指数の定義より、\( 10^3 \) は \( 1000 \) です。その \( 1/10 \) である \( 10^2 \) は \( 100 \) です。その \( 1/10 \) である \( 10^1 \) は \( 10 \) です。さらにその \( 1/10 \) である \( 10^0 \) は \( 1 \) と考えるのが自然です。すべての底について同じことがいえるため、\( a^0 = 1 \) とするのが自然な定義です[2]\( 0^0 = 1 \) と定義すると \( 0^n = 0 \quad (n > 0) \) と矛盾が生じるため、\( 0^0 \) は通常定義されません。\( a \neq 0 \) の条件をつけて \( a^0 = 1 \) … Continue reading。
| 指数 \( x \) | 値 \( 10^x \) |
|---|---|
| 3 | 1000 |
| 2 | 100 |
| 1 | 10 |
| 0 | 1 |
また底をネイピア数 \( e \) とした指数関数 \( e^x \) を自然指数関数と呼びます。自然指数関数には、微分しても変わらないという特徴があります[3]微分して変わらないことを、自然指数関数の定義とする場合もあります。。
$$ \frac{d}{dx} e^x = e^x $$
自然指数関数 \( e^x \) を \( \exp(x) \) と表記する場合もあります。
指数の公式
- 積の指数 $$ a^x \cdot a^y = a^{x + y} \quad (a > 0) $$
- 商の指数 $$ \frac{a^x}{a^y} = a^{x – y} \quad (a > 0) $$
- 累乗の指数 $$ (a^x)^r = a^{xr} \quad (a > 0) $$
- 指数の分配 $$ (ab)^x = a^x \cdot b^x \quad (a > 0, b > 0) $$
- 逆数の指数 $$ a^{-x} = \frac{1}{a^x} \quad (a > 0) $$
