微分 | みんなのデータサイエンス

微分とは

微分とは、関数の変化率を表す数学的な概念です。データサイエンスにおいては、モデルの損失関数を最小化するための勾配降下法や、深層学習における誤差逆伝播法、また最適化アルゴリズムの計算に利用されます^[1] … Continue reading。

微分の基本的な考え方は、関数の入力がわずかに変化したときに、出力がどれだけ変わるかを調べることです。たとえば、関数のある点における接線の傾きは、微分によって求めることができます。この傾きを、微分係数と呼びます。

関数を微分して得られる新しい関数を、導関数と呼びます。関数 $ f(x) $ の導関数は、次のように定義されます^[2]$ f'(x) $ をラグランジュの記法、$ \frac{df}{dx} $ をライプニッツの記法と呼びます。。

$$ f'(x) = \frac{df}{dx} = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h} $$

以下のグラフは、関数 $ f(x) = x^2 $ とその導関数 $ f'(x) = 2x $ を表しています。

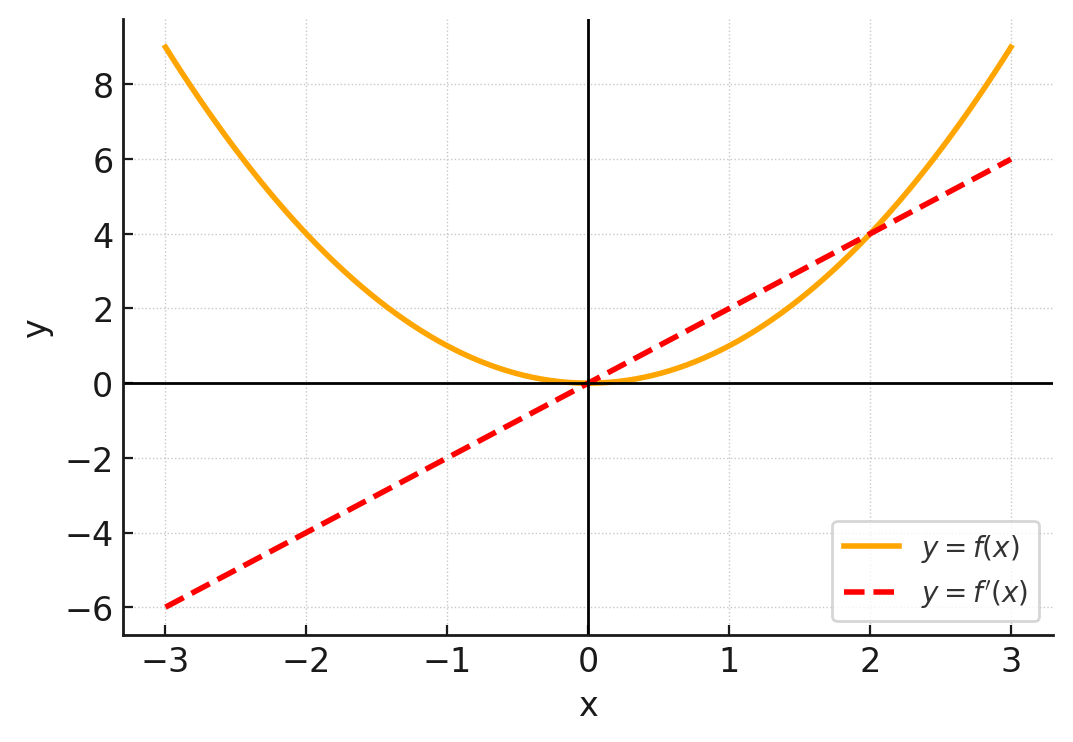
$ x = 1 $ における関数 $ f(x) $ の接線の傾き（微分係数）は、導関数 $ f'(x) = 2x $ に $ x = 1 $ を代入し $2 $ と得られます。

微分係数と導関数は似た概念ですが、次のような違いがあります。

多変数関数に対して、ある変数のみで微分を取ることを偏微分と呼びます。例えば、関数 $ f(x, y) = x^2 + y^2 $ に対して、$ x $ についての偏微分は次のようになります。

$$ \frac{\partial f}{\partial x} = 2x, \quad \frac{\partial f}{\partial y} = 2y $$

定数の微分 $$ \frac{d}{dx} c = 0 $$
べき乗の微分 $$ \frac{d}{dx} x^n = n x^{n-1} $$
和の微分 $$ \frac{d}{dx} (f + g) = \frac{d}{dx} f + \frac{d}{dx} g $$
積の微分 $$ \frac{d}{dx} (f g) = \frac{d f}{dx} g + f \frac{d g}{dx} $$
商の微分 $$ \frac{d}{dx} \left( \frac{f}{g} \right) = \frac{\frac{d f}{dx} g – f \frac{d g}{dx}}{g^2} $$
自然指数関数の微分 $$ \frac{d}{dx} e^x = e^x $$
一般指数関数の微分 $$ \frac{d}{dx} a^x = a^x \ln a \quad (a > 0, a \neq 1) $$
自然対数関数の微分 $$ \frac{d}{dx} \ln x = \frac{1}{x} $$
一般対数関数の微分 $$ \frac{d}{dx} \log_a x = \frac{1}{x \ln a} \quad (a > 0, a \neq 1) $$
三角関数の微分 $$ \frac{d}{dx} \sin x = \cos x, \quad \frac{d}{dx} \cos x = -\sin x, \quad \frac{d}{dx} \tan x = \frac{1}{\cos^2 x} $$
双曲線関数の微分 $$ \frac{d}{dx} \sinh x = \cosh x, \quad \frac{d}{dx} \cosh x = \sinh x, \quad \frac{d}{dx} \tanh x = \frac{1}{\cosh^2 x} $$
合成関数の微分（連鎖律） $$ \frac{d}{dx} f(g(x)) = \frac{d f}{d g} \cdot \frac{d g}{dx} $$
逆関数の微分 $$ \frac{dy}{dx} = \frac{1}{\frac{dx}{dy}} $$

脚注[+]

脚注
1	解析解（数学的に厳密な解）を求めることができない場合も多く、近似解やヒューリスティック解（経験則に基づく実用性を重視した解）を求めるための各種手法が考案されています。
2	$ f'(x) $ をラグランジュの記法、$ \frac{df}{dx} $ をライプニッツの記法と呼びます。