関数とは
関数(function)とは、ある入力に対して一定の規則で出力を返す仕組みのことを指します。AI(人工知能)のモデルも関数の一種と考えることができます。
\( x \) を入力変数、\( y \) を出力変数とする関数 \( f(x) \) は次のように表現されます。
$$ y = f(x) $$
各種の関数
データサイエンスでよく用いられる関数には、以下のようなものがあります。
一次関数
一次関数(linear function)は、線形回帰分析のようにデータの傾向を直線で表す場合に使われます。線形関数やアフィン関数(affine function)とも呼ばれます
$$ f(x) = ax + b $$
一次関数の例をグラフで示します。
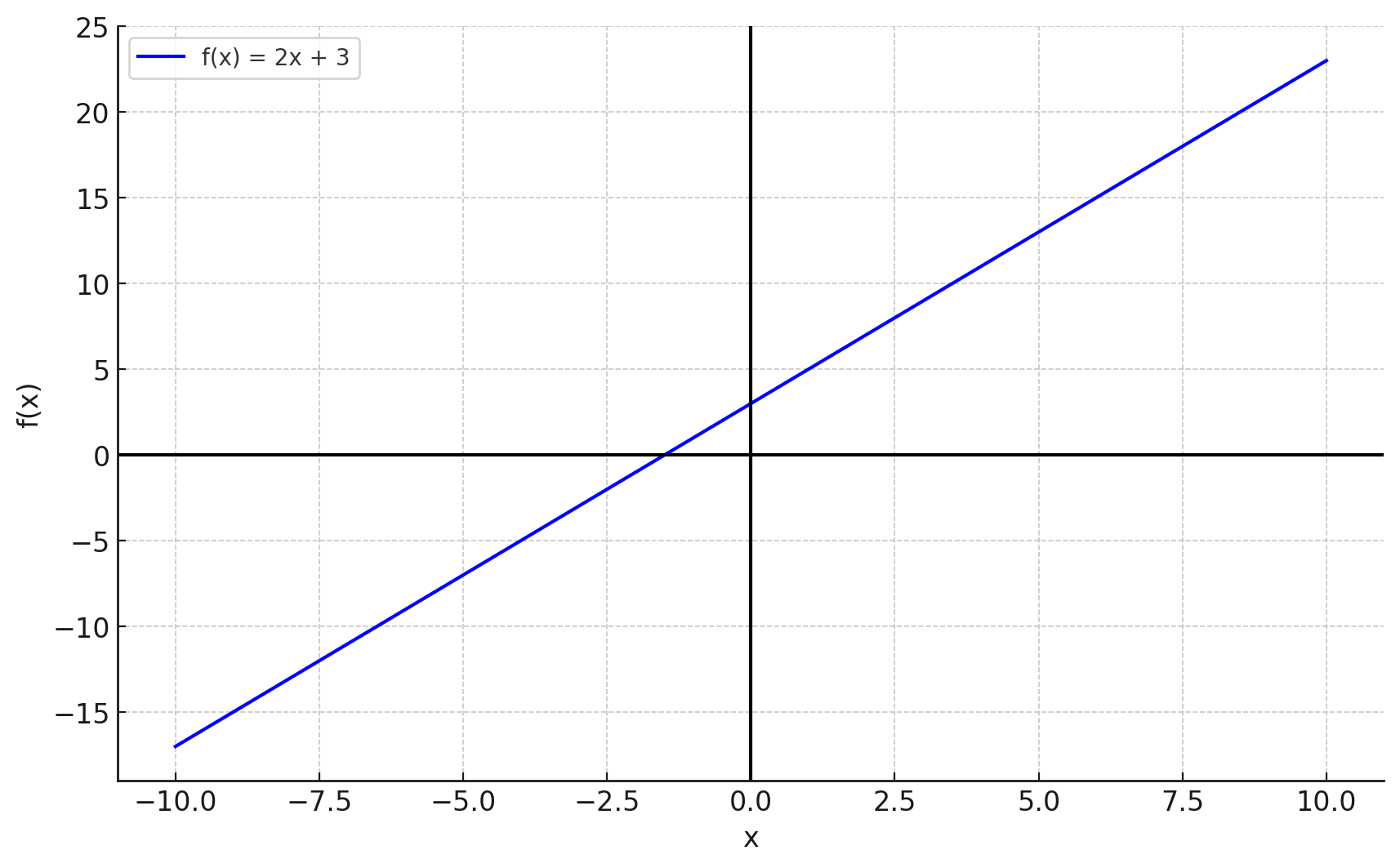
二次関数
二次関数(quadratic function)は、放物線の形をしており、二次回帰(二次の多項式回帰)などで使われます。
$$ f(x) = ax^2 + bx + c $$
二次関数の例をグラフで示します。
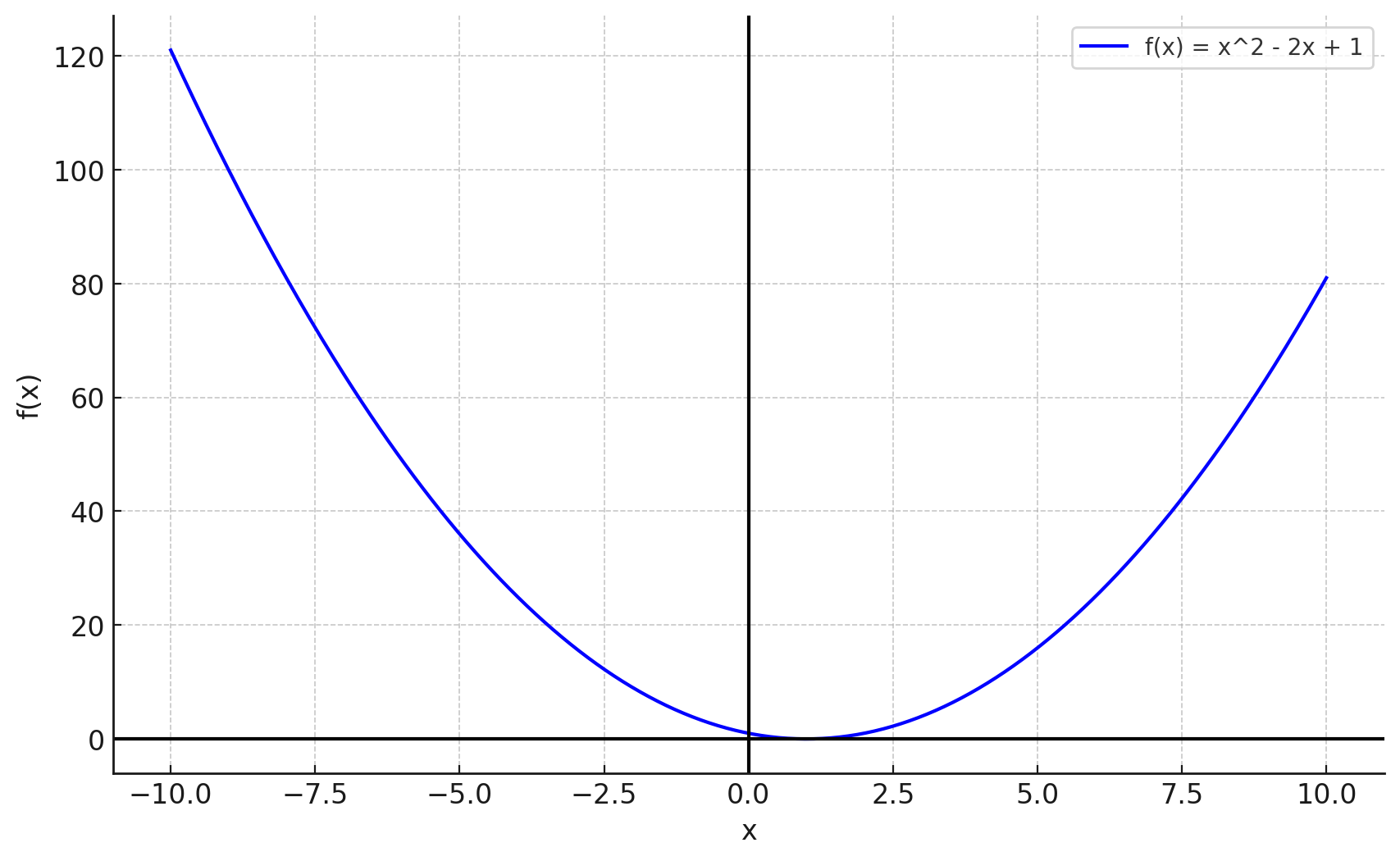
指数関数
指数関数(exponential function)は、成長や減衰を表現するのに使われます。例えば、人口増加や放射性物質の減衰に適用されます。
$$ f(x) = a^x $$
指数関数の例をグラフで示します。
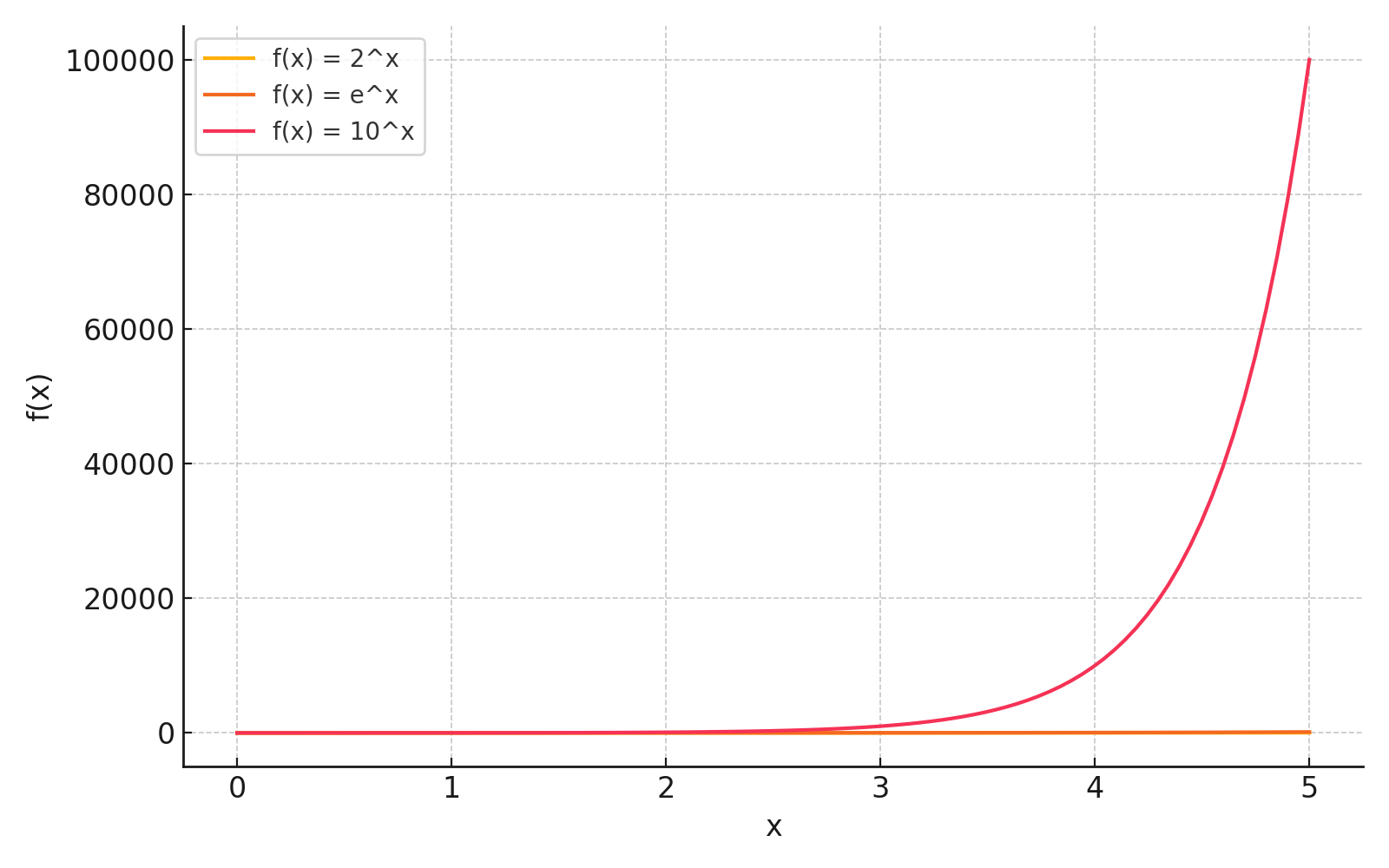

対数関数
対数関数(logarithmic function)は、指数関数の逆関数として定義され、スケールの大きなデータを圧縮するためによく使われます。
$$ f(x) = \log_b x $$
対数関数の例をグラフで示します。
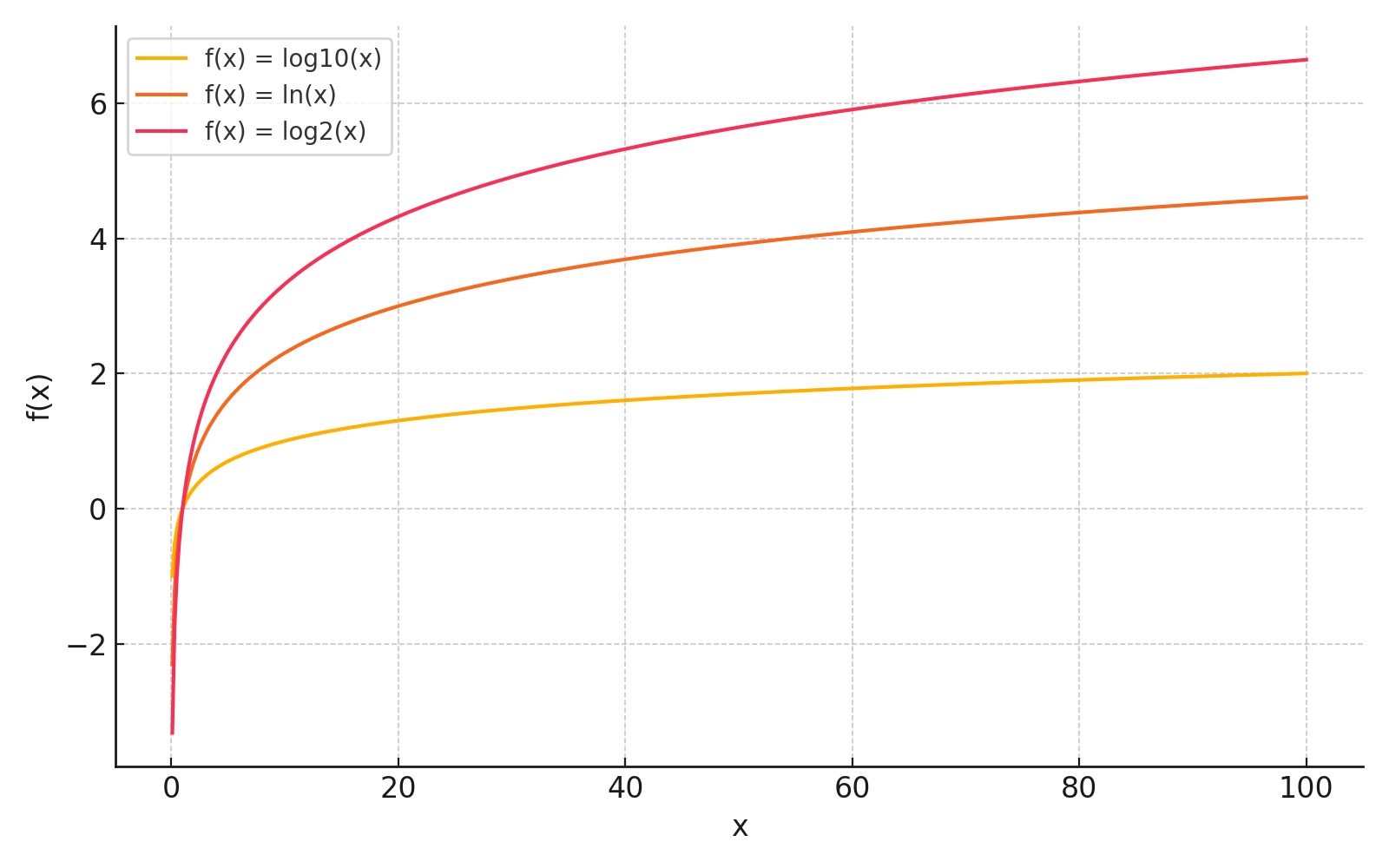

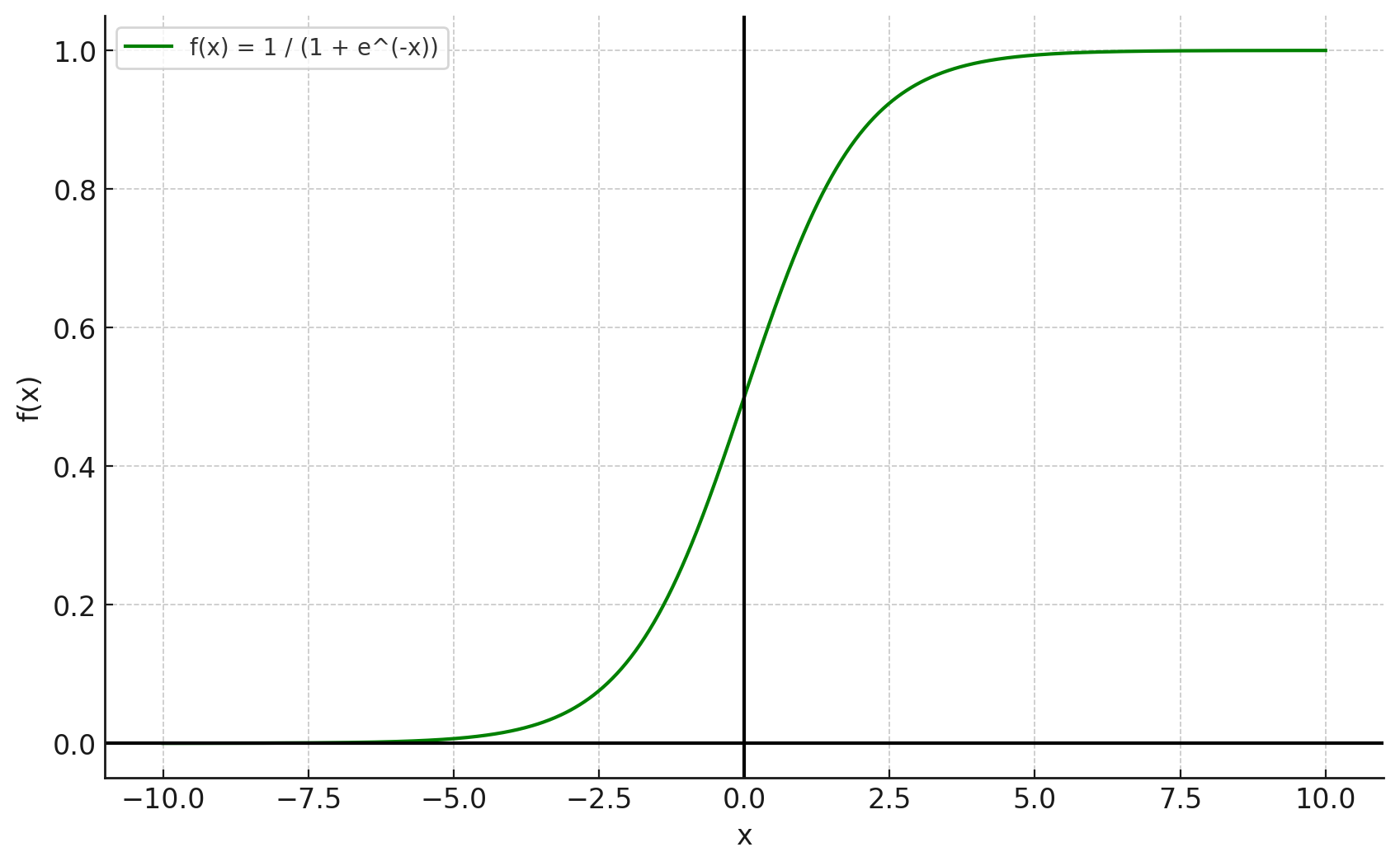
シグモイド関数
シグモイド関数(sigmoid function)は、ロジスティック回帰や、深層学習の活性化関数として使用されます。出力が0から1の範囲に収まる特徴を持ちます。
$$ f(x) = \frac{1}{1 + e^{-x}} $$
シグモイド関数の例をグラフで示します。
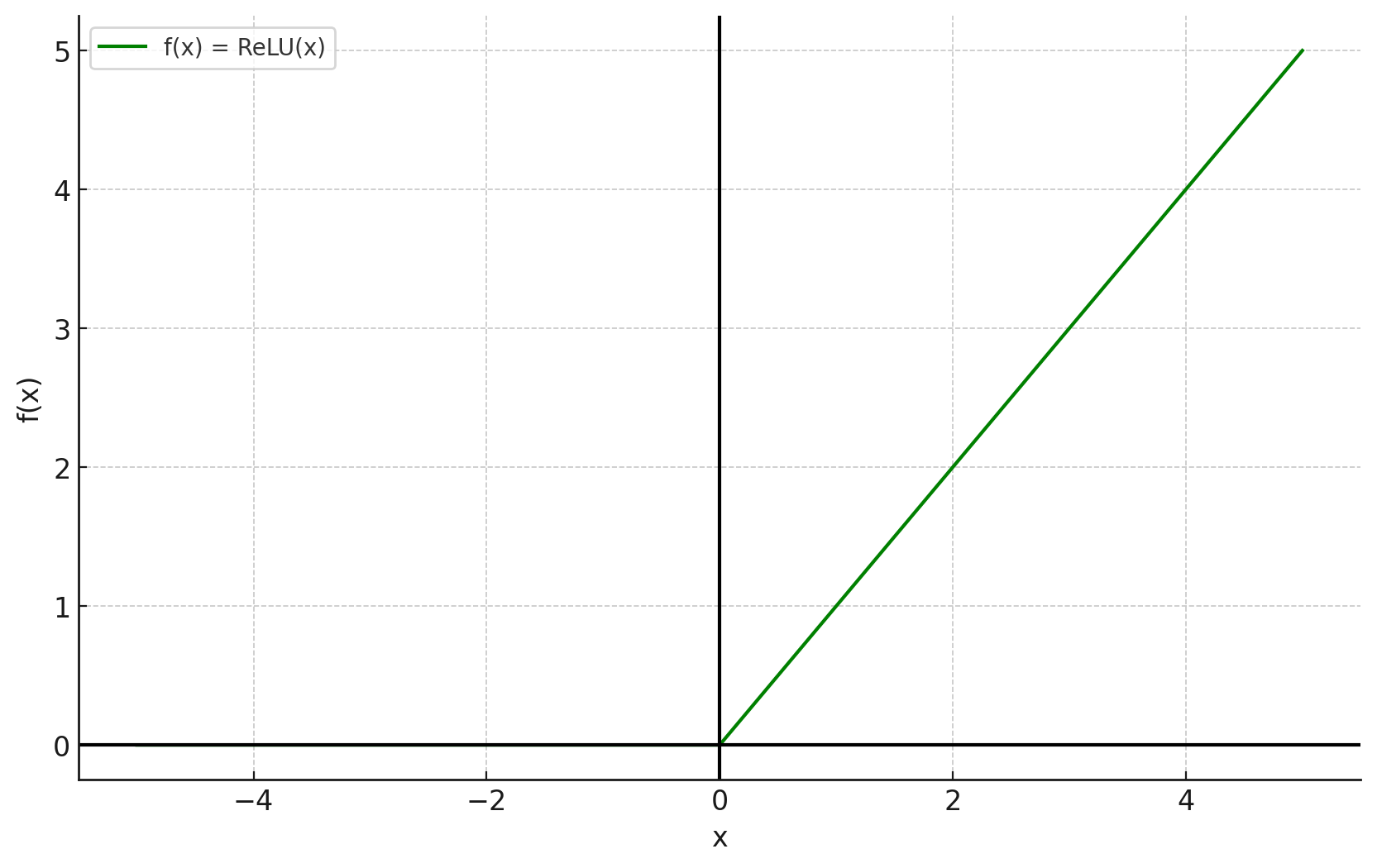
ReLU関数
ReLU関数(ReLU function)は、深層学習の活性化関数としてよく使用されます。入力が正の場合はそのまま出力し、負の場合は0を出力する特性を持ちます。
$$ f(x) = \max(0, x) $$
ReLU関数の例をグラフで示します。
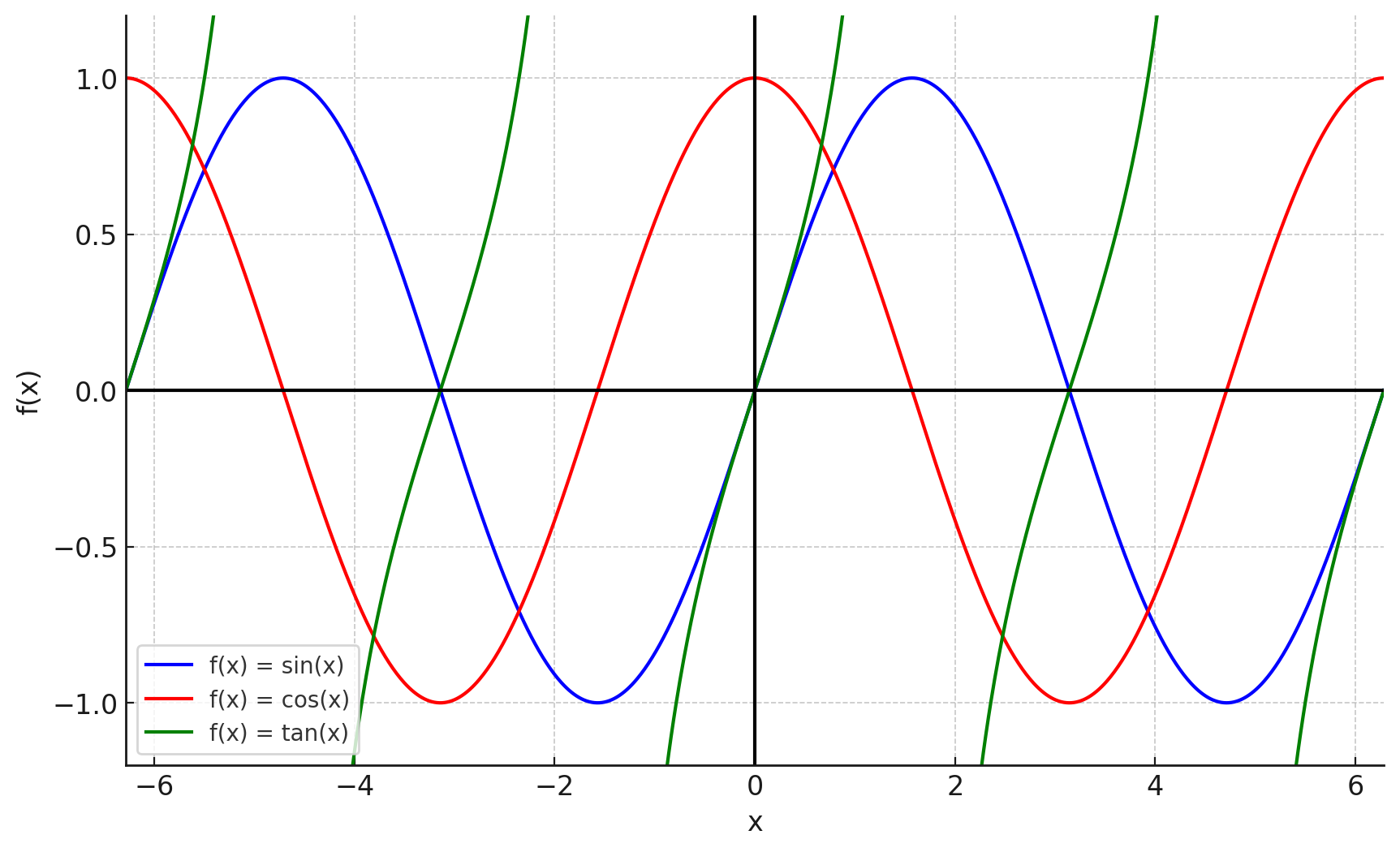
三角関数
三角関数(trigonometric function)は、周期的な変化を表現するのに適した関数です。代表的な三角関数には以下の3つがあります。
- サイン関数(sin):波のような周期的な変化を持つ。
- コサイン関数(cos):サイン関数と位相が90度異なる周期関数。
- タンジェント関数(tan):サイン関数とコサイン関数の比で定義される関数。
三角関数の例をグラフで示します。
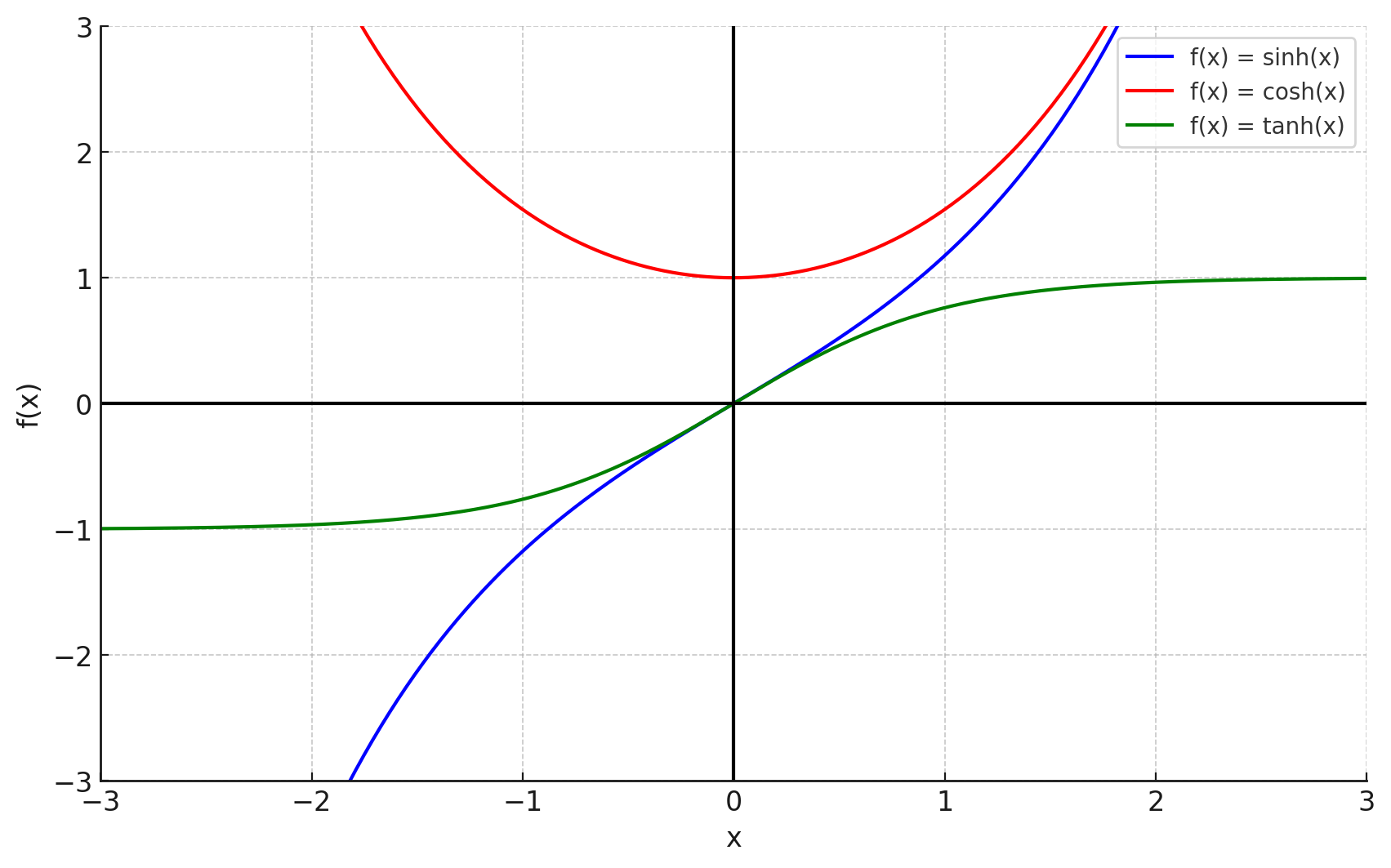
双曲線関数
双曲線関数(hyperbolic function)は、指数関数を基に定義される関数です。代表的な双曲線関数には以下の3つがあります。
- 双曲線サイン関数(sinh):$$ \sinh(x) = \frac{e^x \mathbin{-} e^{-x}}{2} $$
- 双曲線コサイン関数(cosh):$$ \cosh(x) = \frac{e^x + e^{-x}}{2} $$
- 双曲線タンジェント関数(tanh):$$ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x \mathbin{-} e^{-x}}{e^x + e^{-x}} $$
双曲線関数の例をグラフで示します。
合成関数
合成関数(composite function)は、複数の関数を組み合わせて新しい関数を作る手法です。ニューラルネットワークの各層では、活性化関数と線形関数を組み合わせることで、複雑なモデルを構築します。
数学的には、関数 \( f(x) \) と \( g(x) \) を組み合わせて新しい関数 \( h(x) \) を作ることを次のように表します。
$$ h(x) = f(g(x)) $$
また合成関数の表記方法として、次のように \( \circ \) を用いる場合もあります。
$$ h = f \circ g $$
例えば、\( g(x) = 2x + 3 \) (線形関数)と \( f(x) = \frac{1}{1 + e^{-x}} \) (シグモイド関数)の場合、合成関数は以下のようになります。
$$ h(x) = \frac{1}{1 + e^{-(2x + 3)}} $$
このように、合成関数を活用することで、単純な関数の組み合わせから複雑な関数を構築することができます。
逆関数
逆関数(inverse function)とは、ある関数の出力から元の入力を求めるための関数です。つまり、関数 \( f(x) \) があるとき、その逆関数 \( f^{-1}(x) \) は次の関係を満たします。
$$ f^{-1}(f(x)) = x $$
これは、「関数を適用したあとに逆関数を適用すると元に戻る」ことを意味します。
逆関数の有名な例として、指数関数と対数関数があります。
- 指数関数: \( f(x) = e^x \)
- 逆関数: \( f^{-1}(x) = \ln(x) \)
すべての関数に逆関数が存在するわけではありません。例えば、二次関数 \( f(x) = x^2 \) は、入力の正負によって同じ値になるため、逆関数を一意に定義できません。
このような場合、特定の範囲に制限することで逆関数を定義できることがあります。例えば、\( x \geq 0 \) の範囲で考えれば、\( f^{-1}(x) = \sqrt{x} \) となります。
まとめ
関数はデータサイエンスの基礎を成す重要な概念であり、機械学習や統計解析において広く活用されています。AIの本質も関数としての振る舞いに他なりません。関数の種類や性質を理解することで、データサイエンスの応用範囲を広げることができるでしょう。


